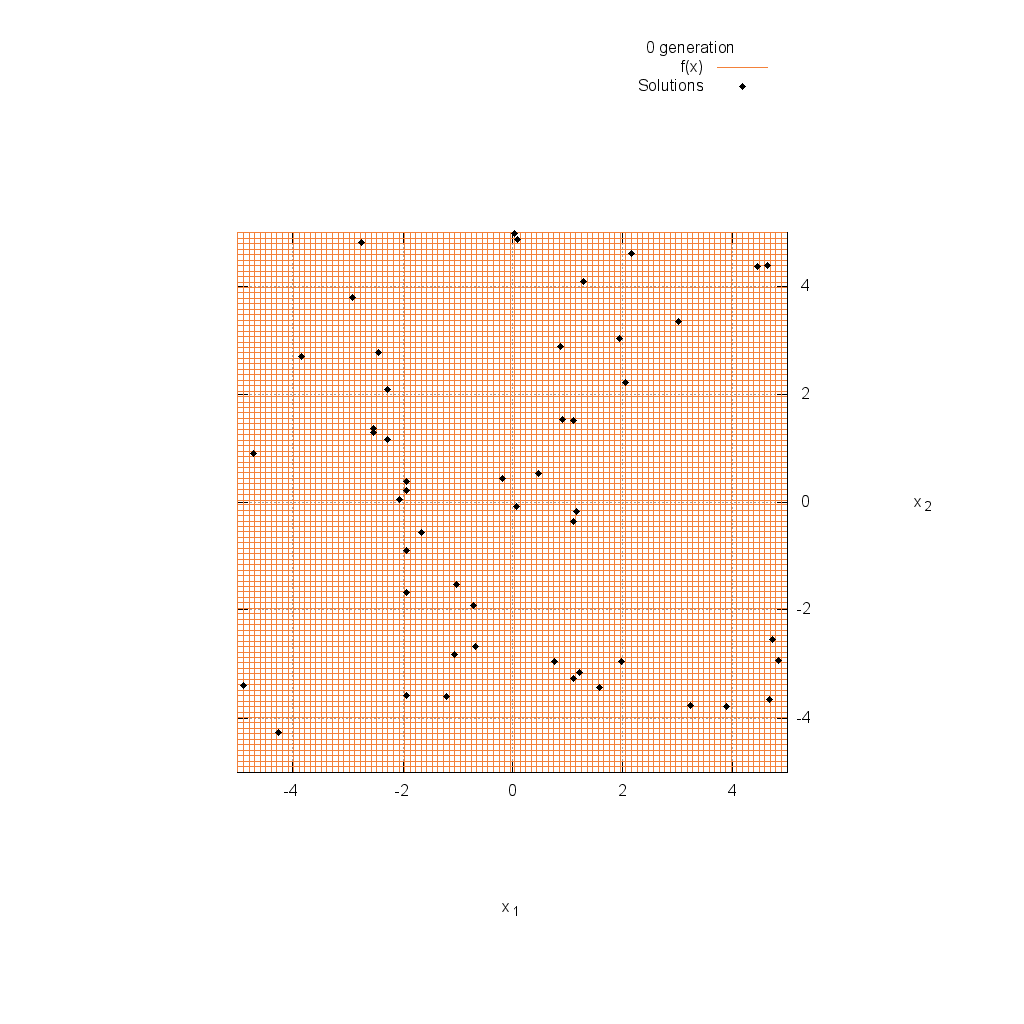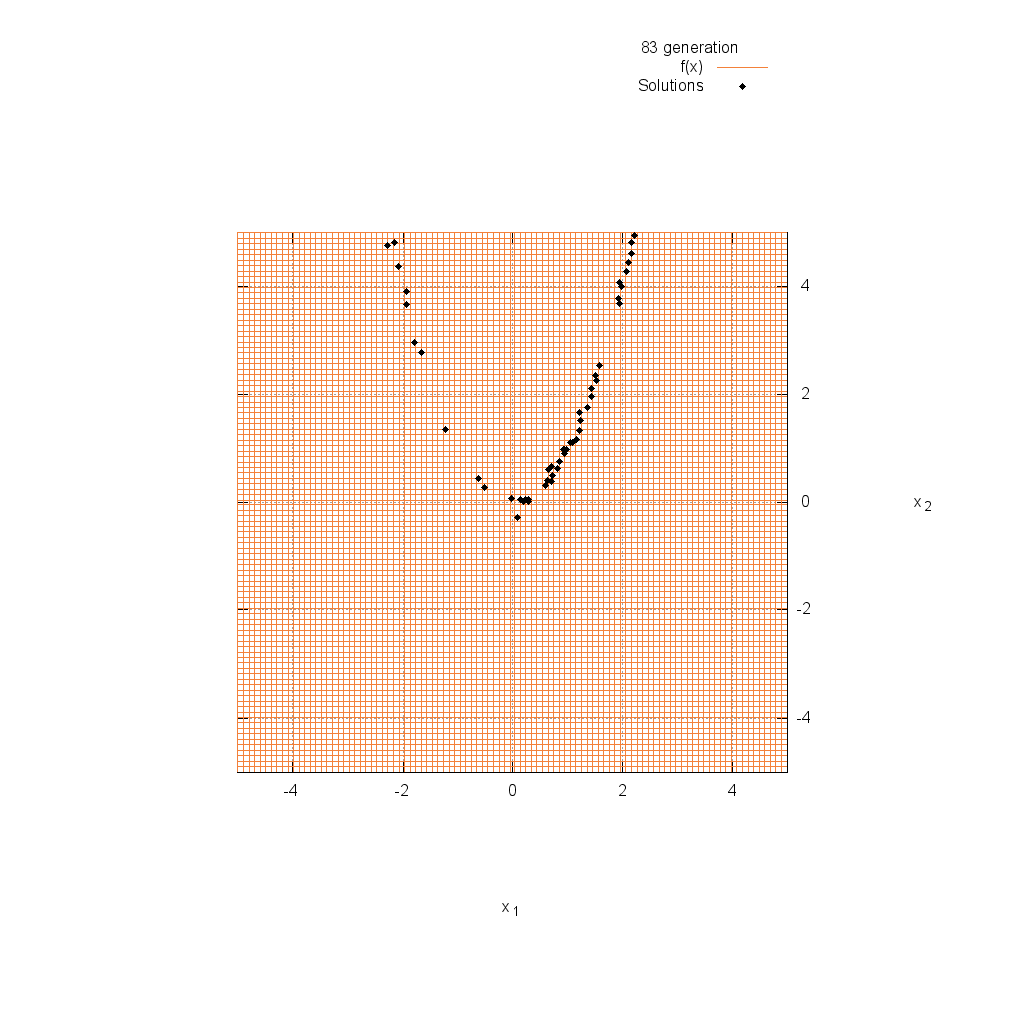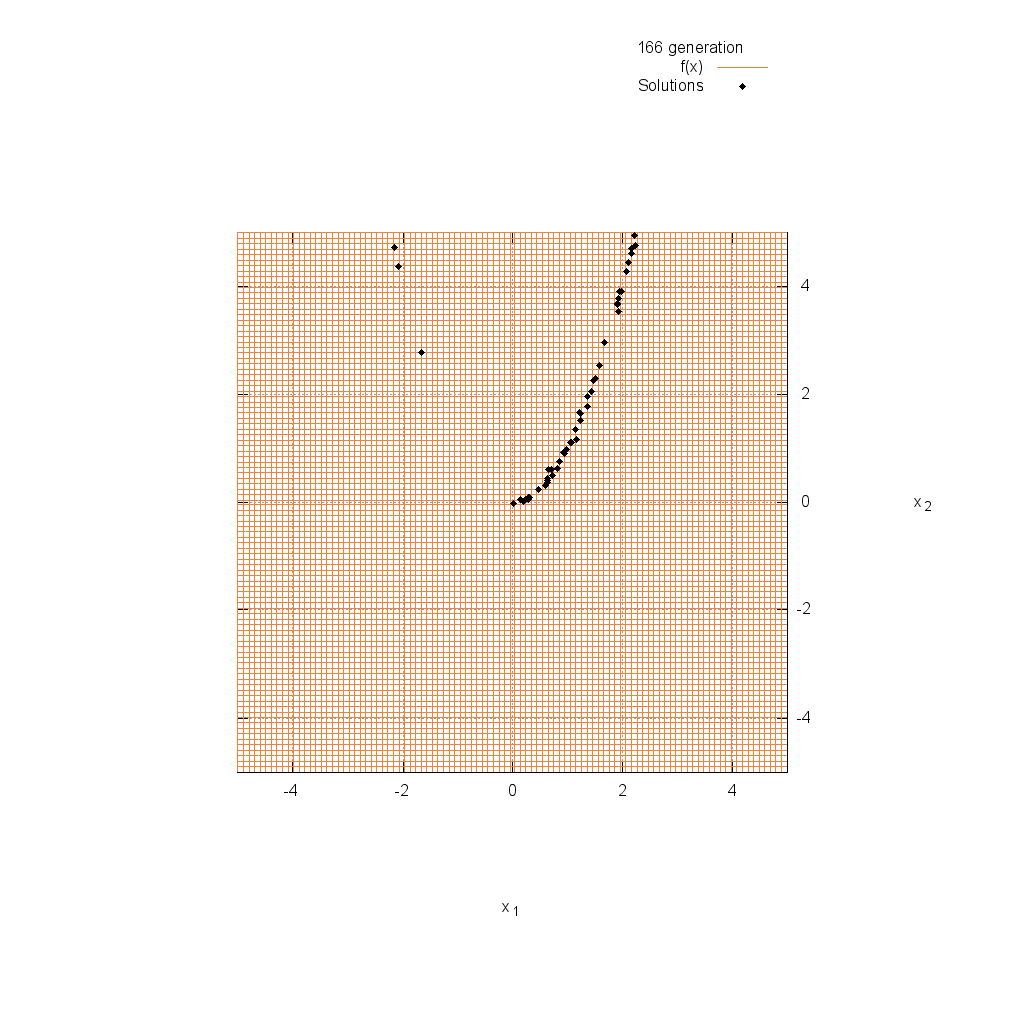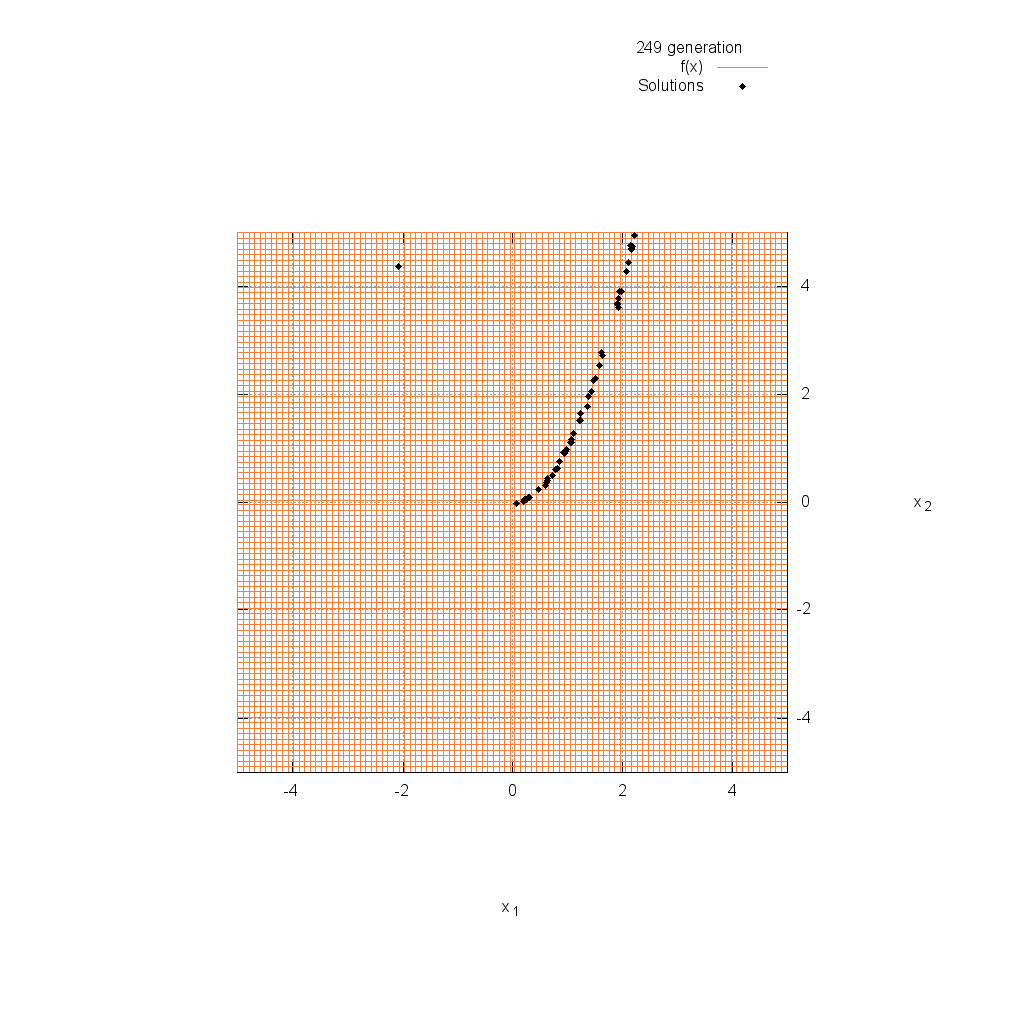
プログラミング:佐藤 尊樹
はじめに
解が実数値で表現される最適化問題において,近年,注目される最適化法のひとつが差分進化(Differential Evolution, DE)です.ここでは簡単にDEを紹介します.
差分進化 (Differential Evolution)
解は実数値ベクトル\(\boldsymbol{x}={x_1,x_2,\cdots,x_n}\)で表します.世代数\(t\)に対し,解集団\(\mathcal{P}_t=\{\boldsymbol{x}_{1,t},\boldsymbol{x}_{2,t},\cdots,\boldsymbol{x}_{N,t}\}\)をランダムに生成します.各\(\boldsymbol{x}_{i,t}\)に対して,次式で変異ベクトルを算出します.
$$\boldsymbol{v}_{i,t}=\boldsymbol{x}_{r_1,t}+F\cdot(\boldsymbol{x}_{r_2,t}-\boldsymbol{x}_{r_3,t})$$
ここで,\(F\)はスケーリング係数,\(\boldsymbol{x}_{r_1,t}\),\(\boldsymbol{x}_{r_2,t}\),\(\boldsymbol{x}_{r_3,t}\)は,解集団からランダムに取り出した解です. 次に\(\boldsymbol{x}_{i,t}\)と変異ベクトル\(\boldsymbol{v}_{i,t}\)を次式のように交叉させることで,新しい解\(\boldsymbol{u}_{i,t}\)を生成します.これを各\(\boldsymbol{x}_{i,t}\)について繰り返します.
$$u_{j,i,t+1}=\left\{\begin{array}{l} v_{j,i,t}&\text{if }\text{rand}[0,1) \le CR\text{ or } j=j_{rand}\\ x_{j,i,t}&\text{otherwise}\end{array}\text{ }(j=1,2,\cdots,n)\right.$$
次に,解集団を更新します.各解\(\boldsymbol{x}_{i,t}\)と新しい解\(\boldsymbol{u}_{i,t}\)を比較し,目的関数値が良好な方を次世代の解集団に残します.
$$\boldsymbol{x}_{i,t+1}=\left\{\begin{array}{l} \boldsymbol{u}_{i,t} &\text{if } f(\boldsymbol{u}_{i,t})\le f(\boldsymbol{x}_{i,t})\\ \boldsymbol{x}_{i,t}&\text{otherwise}\end{array}\right.$$
上記を世代数\(t\)を計数しながら繰り返します.これはDEのひとつの方法で,rand/1/binと表します.
実験
関数最適化問題におけるDEの動作を紹介します.使用した方法は,前述のrand/1/binで,解集団サイズは50,世代数は250,スケーリング係数F=0.7,交叉率CR=0.9に設定しました.
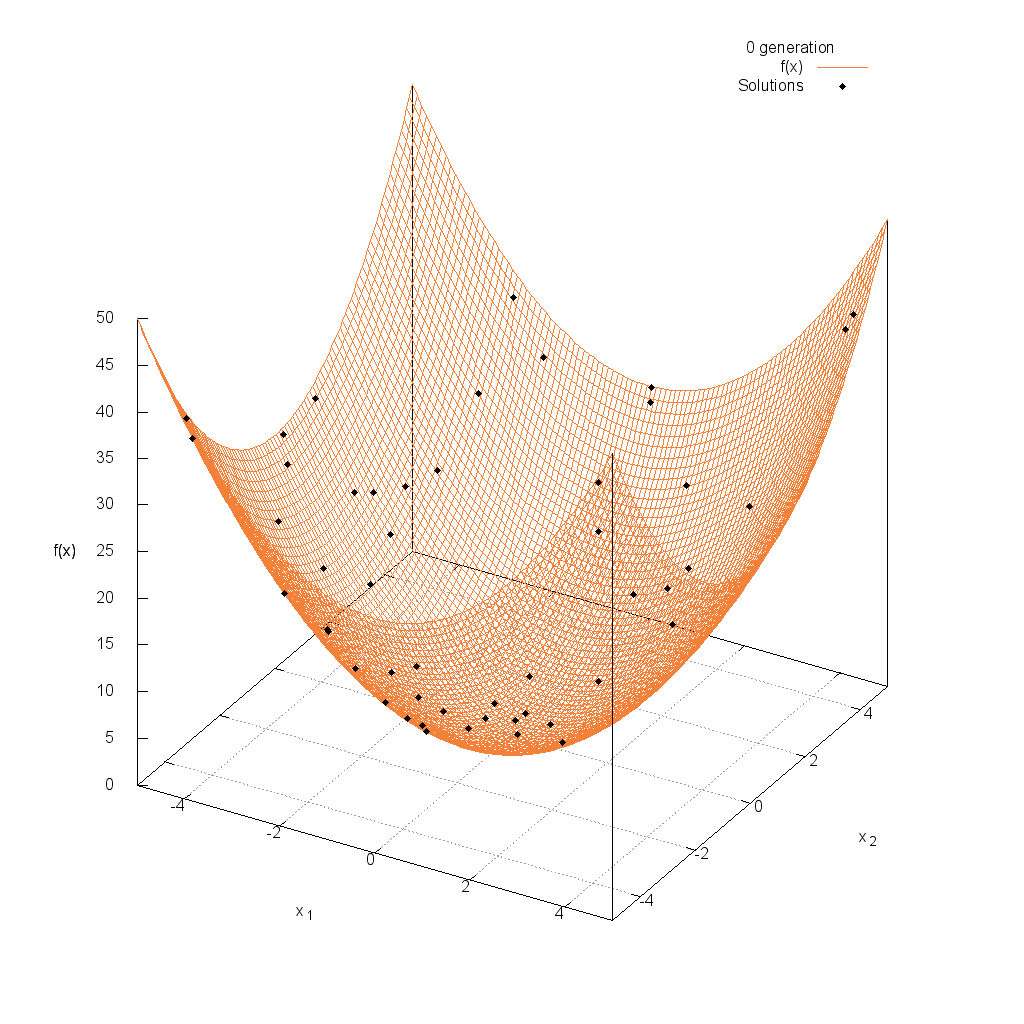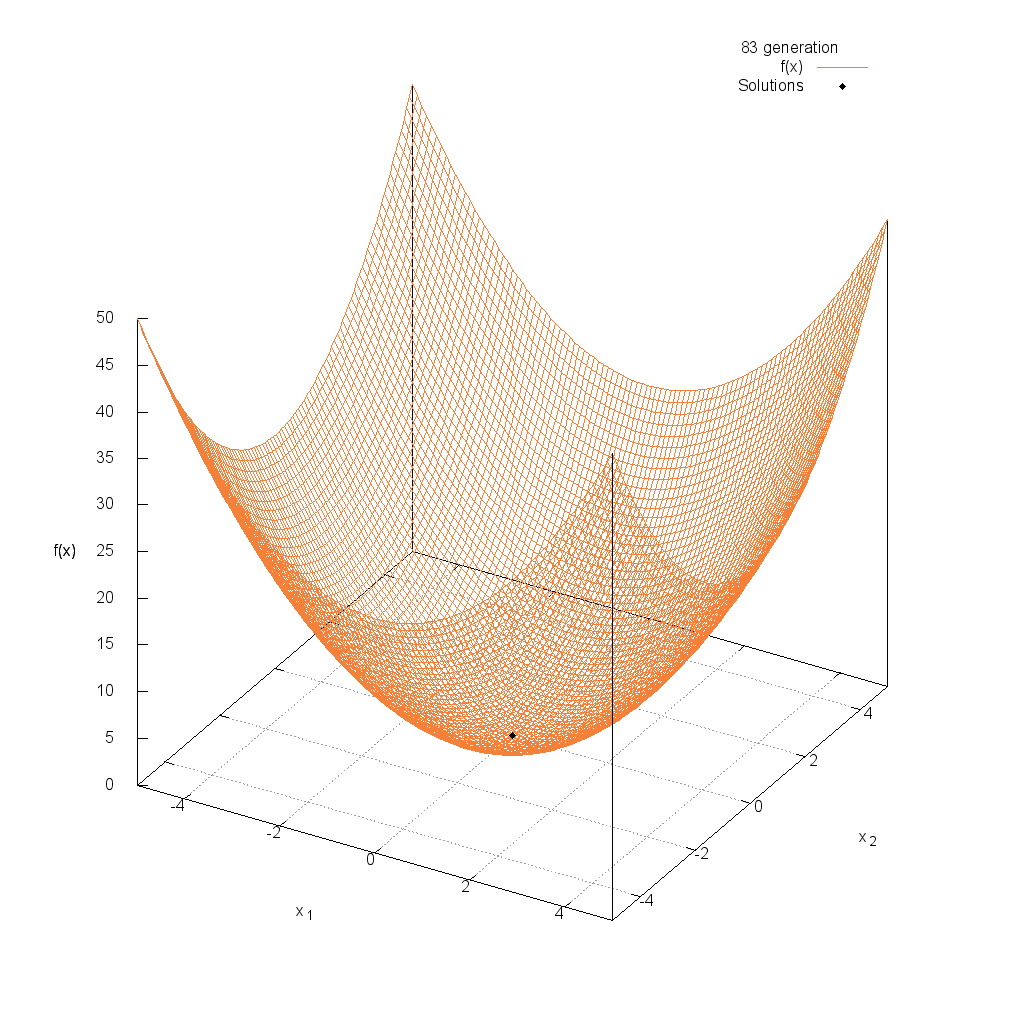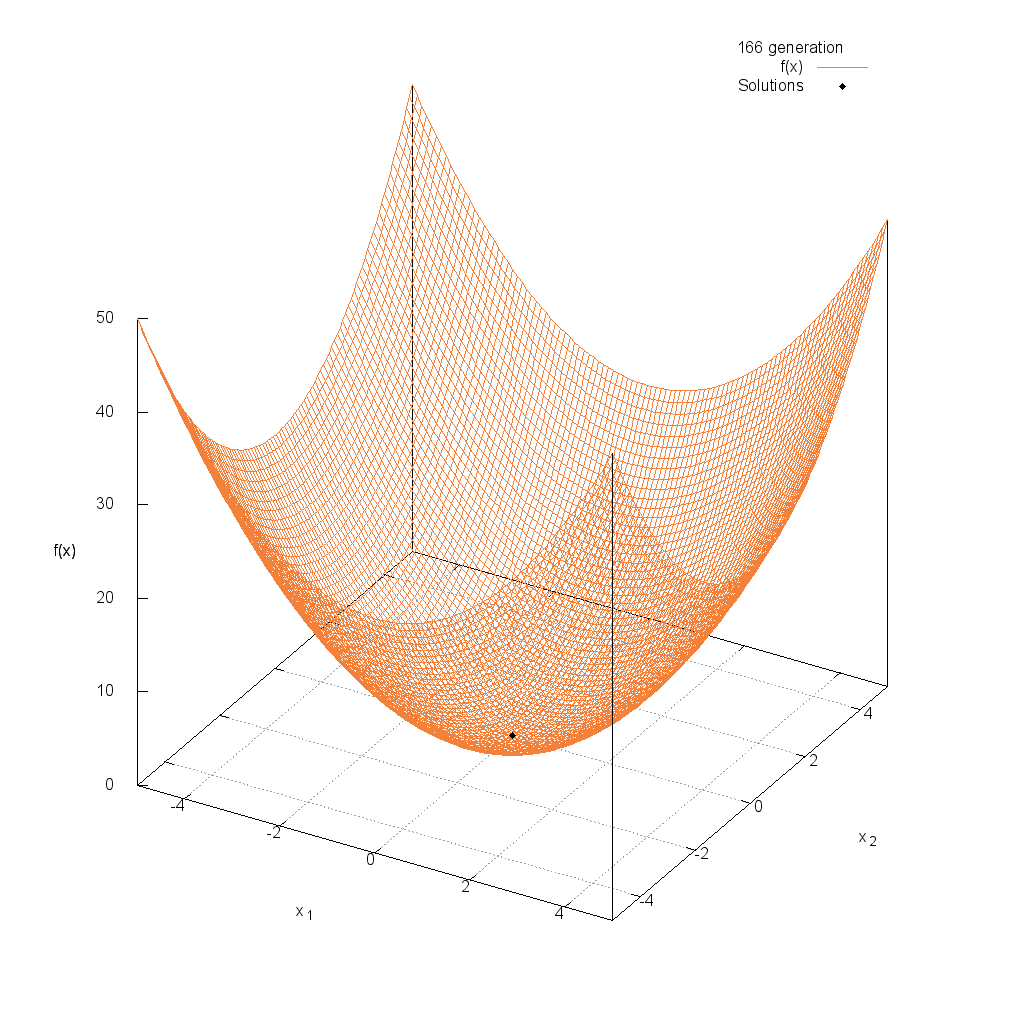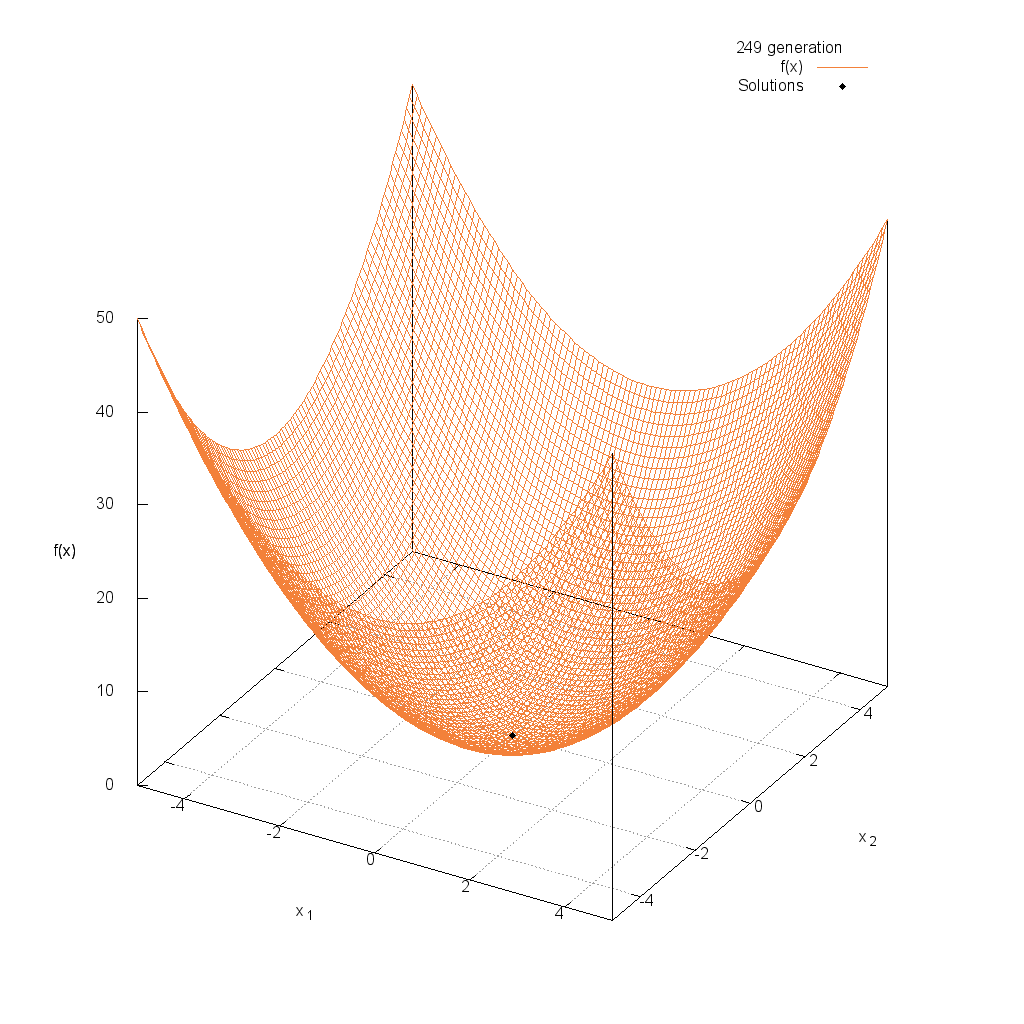
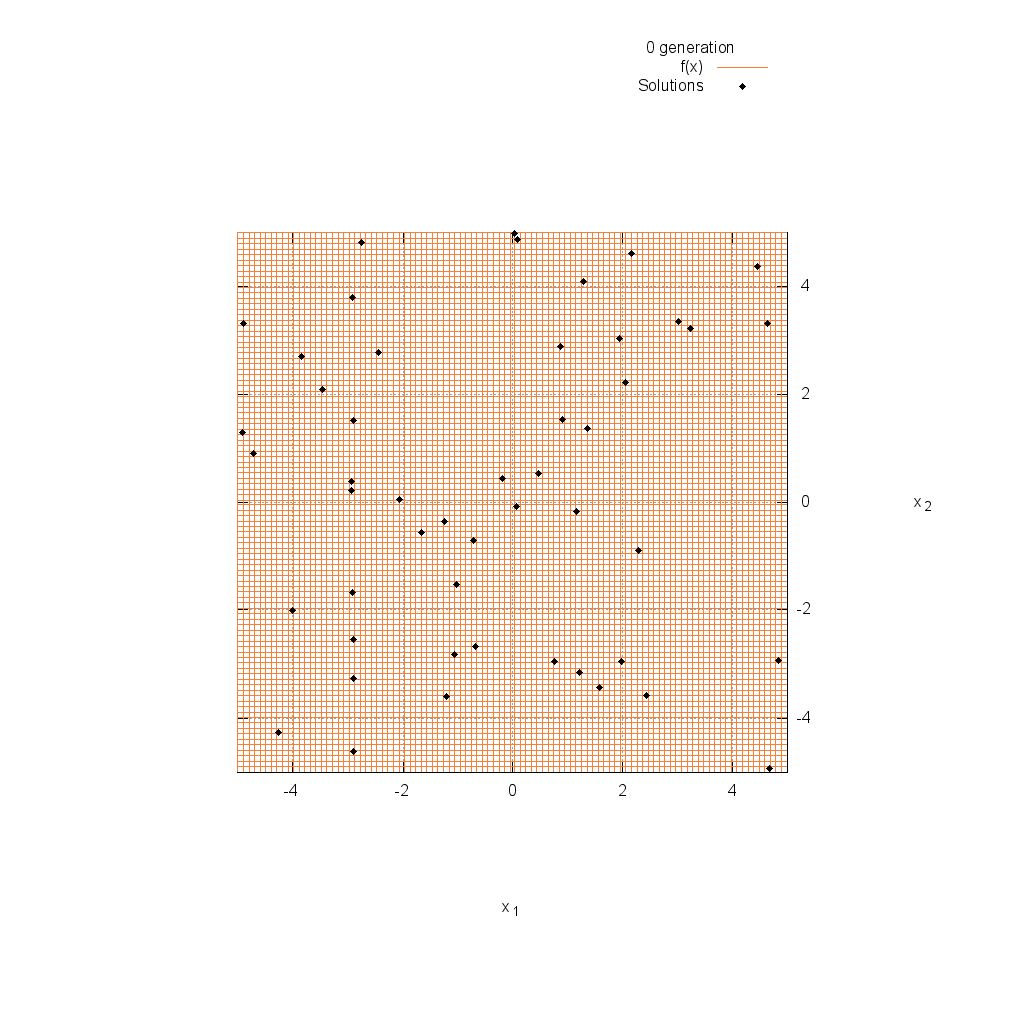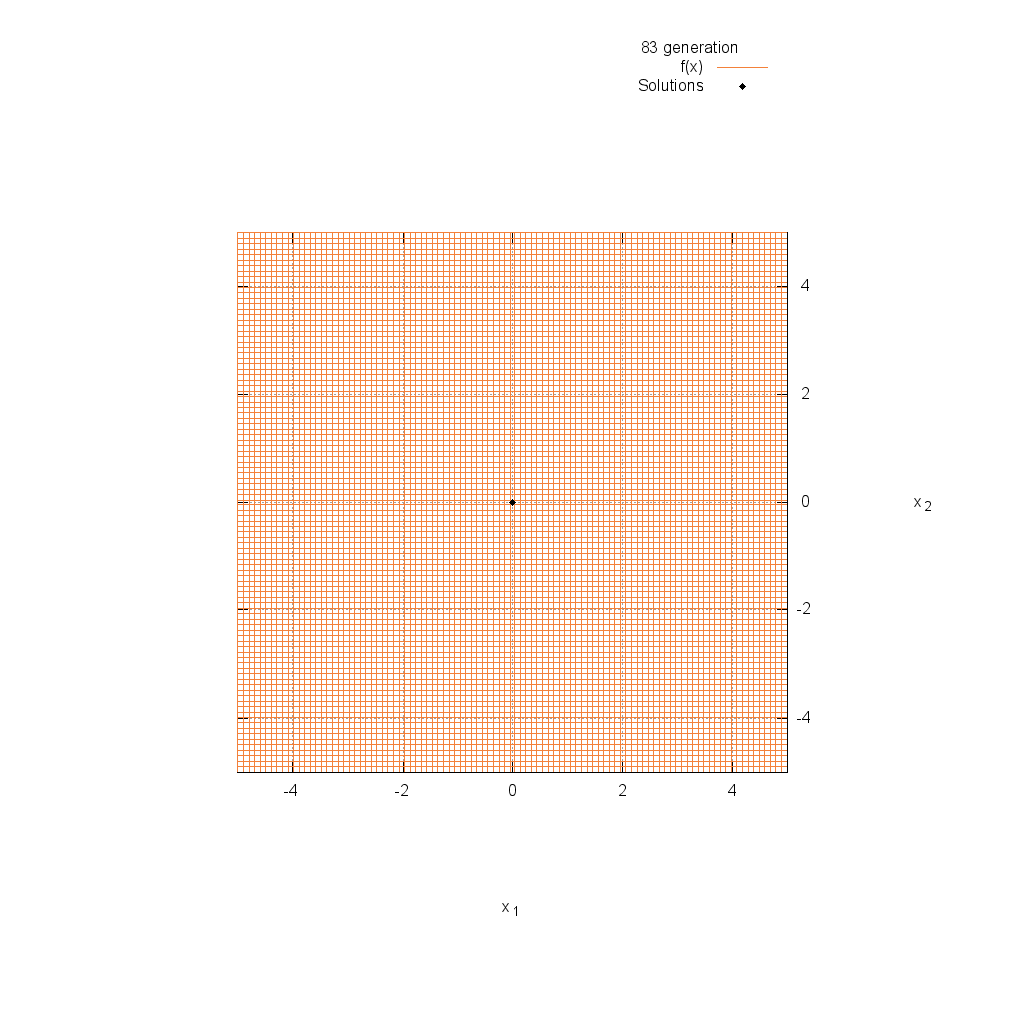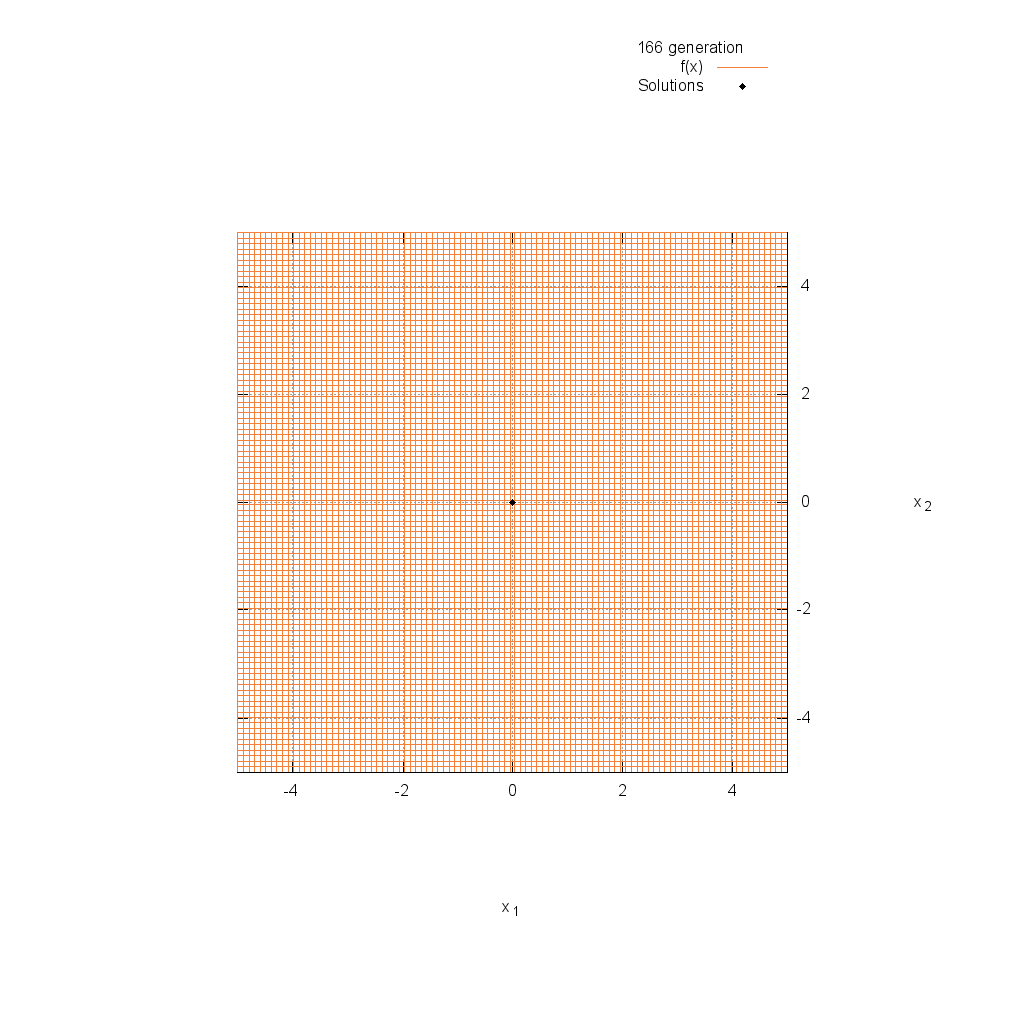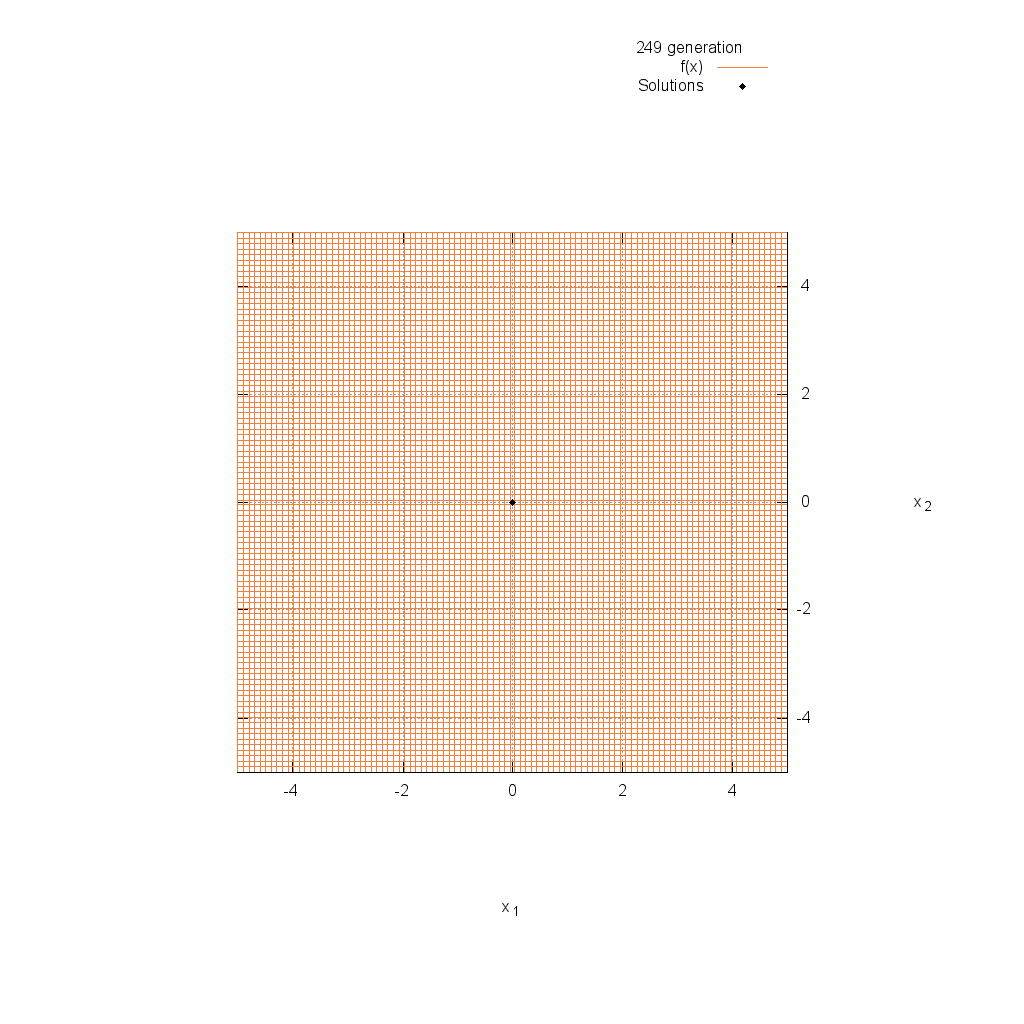
Sphere関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = \sum_{i=1}^n x_i^2$$
$$-5.12 \leq x_i \leq 5.12$$
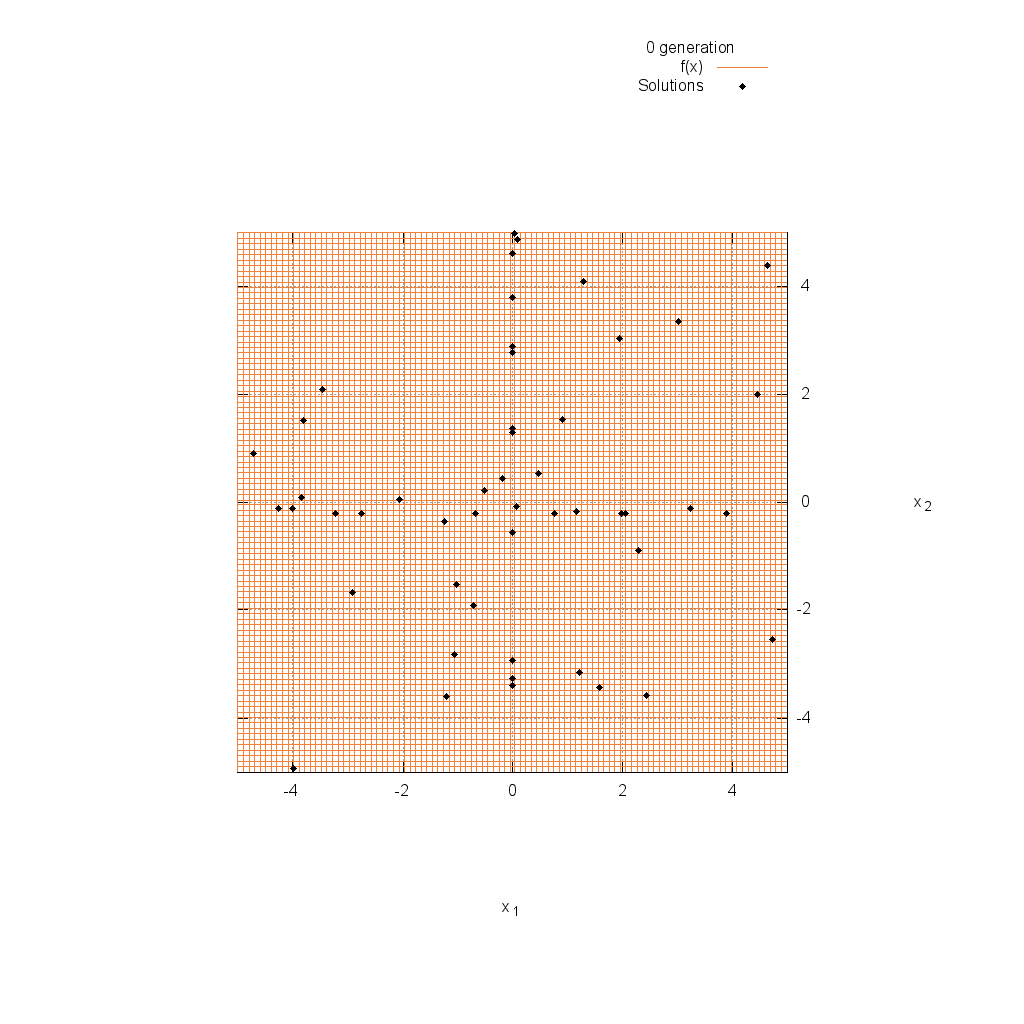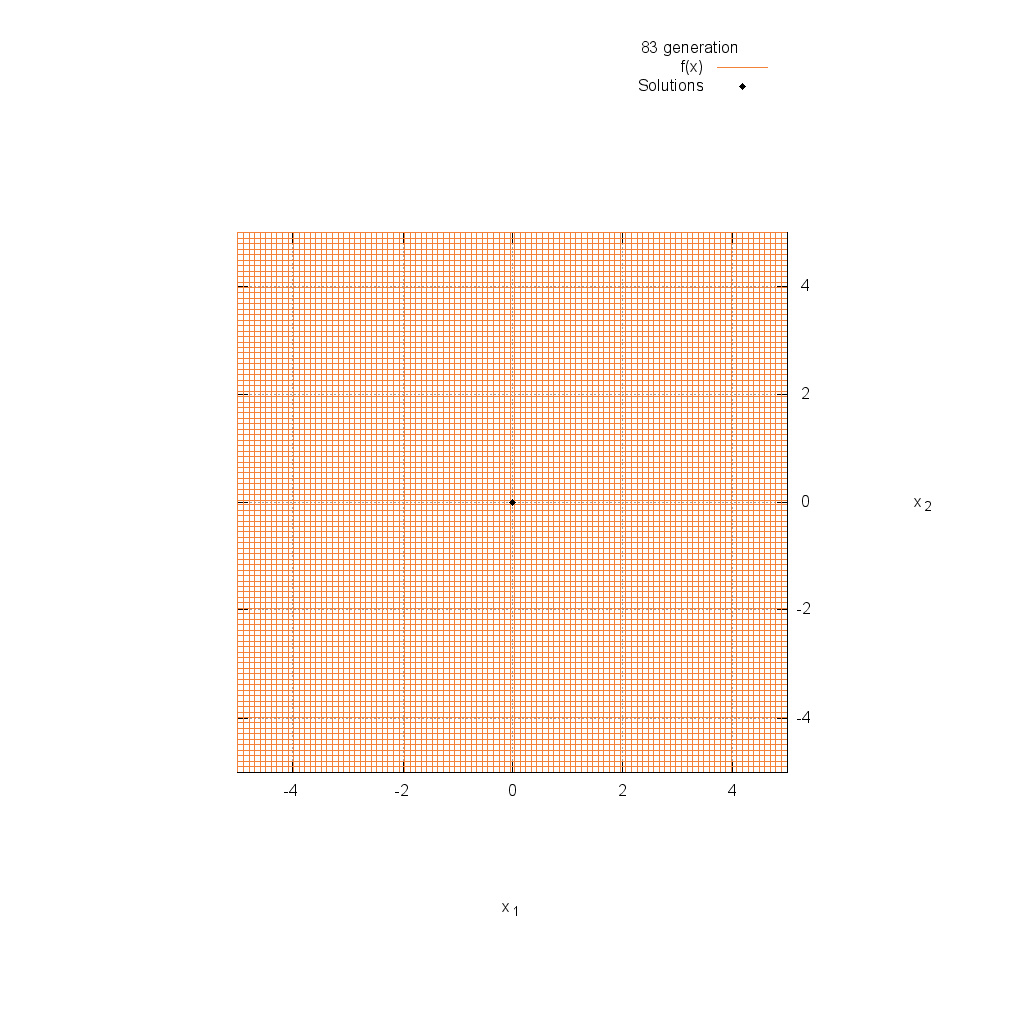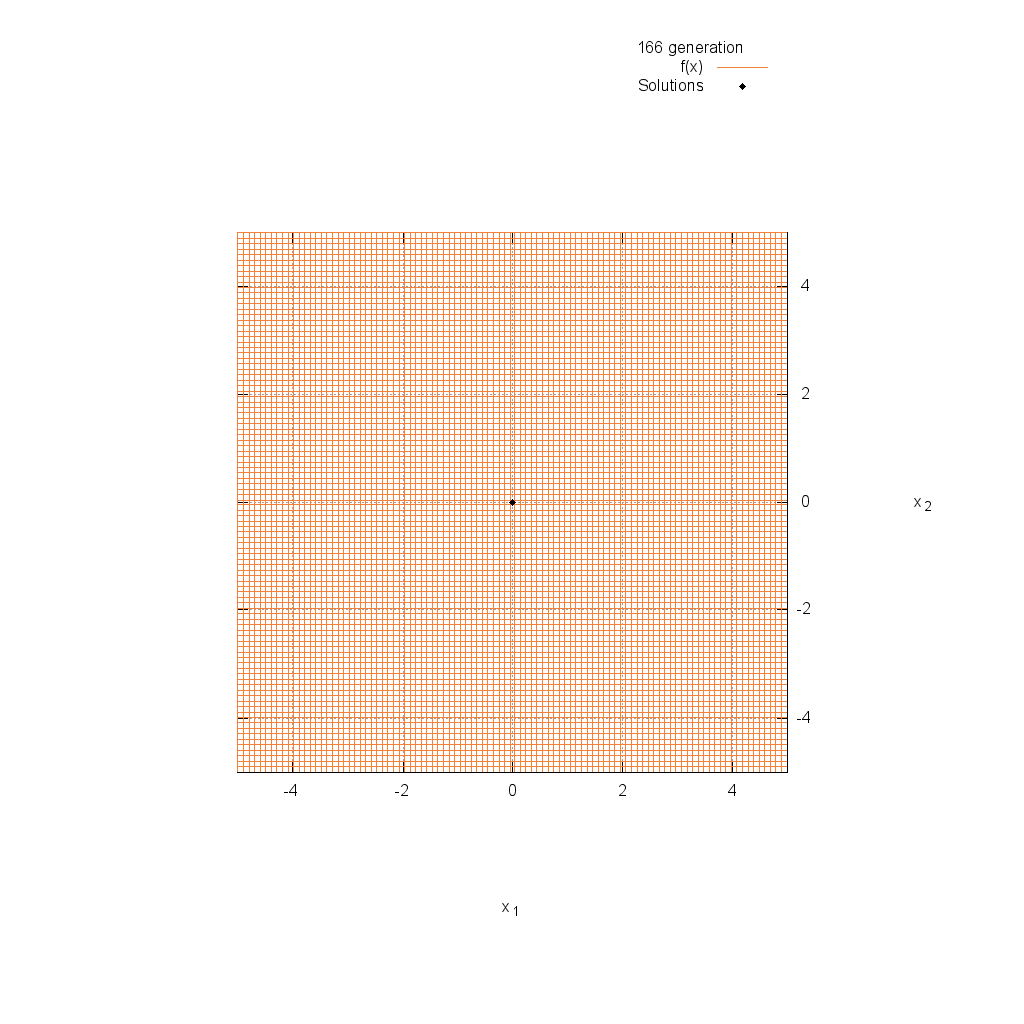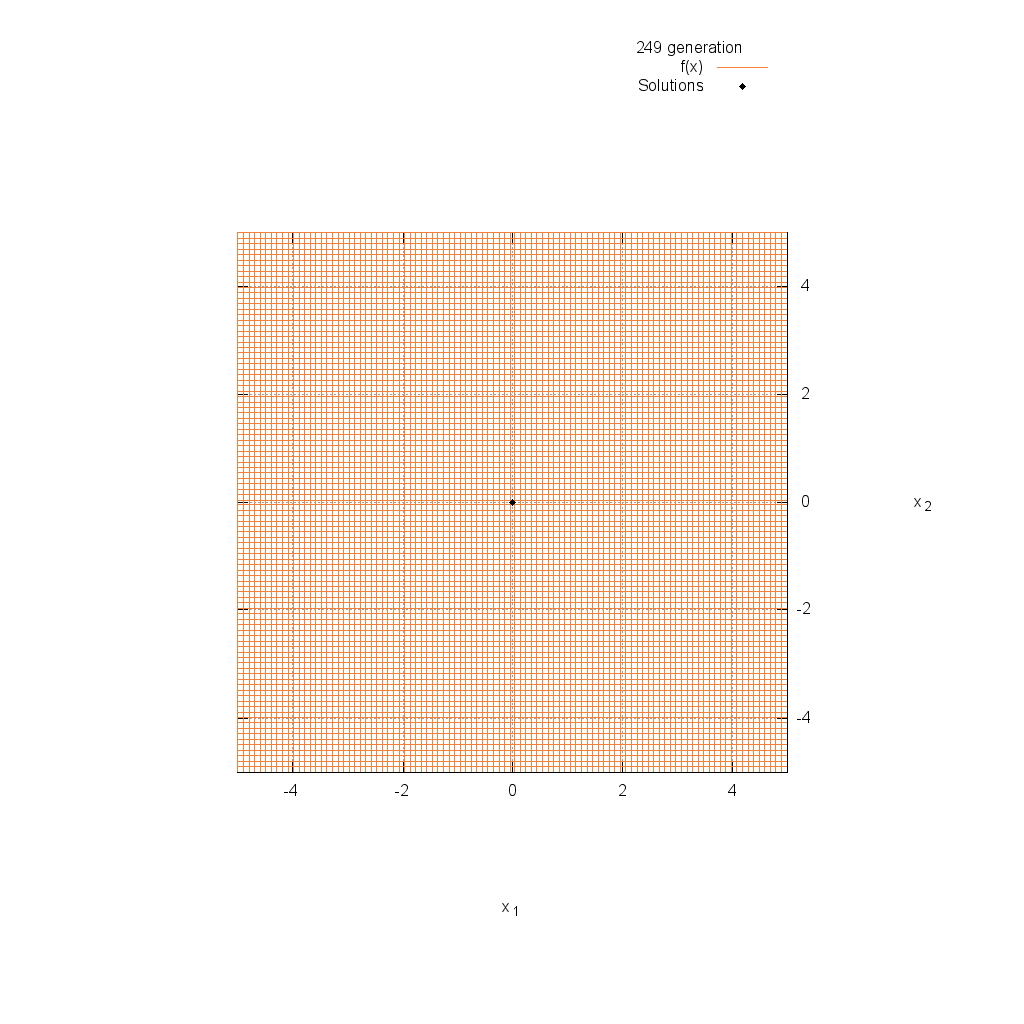
Ackley関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = -20 \exp(-0.2 \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}) – \exp(\frac{1}{n} \sum_{i=1}^n \cos(2\pi x_i)) + 20 + \exp(1)$$
$$-32 \leq x_i \leq 32$$
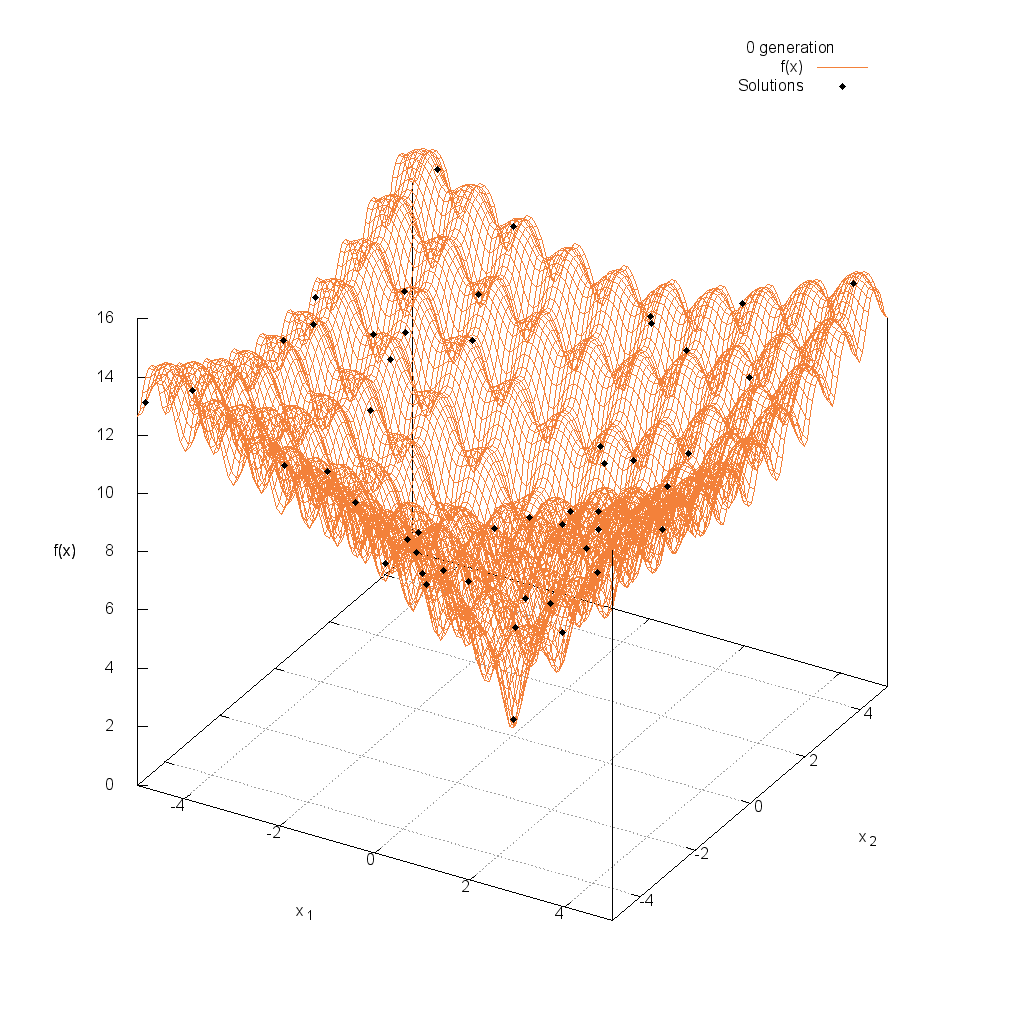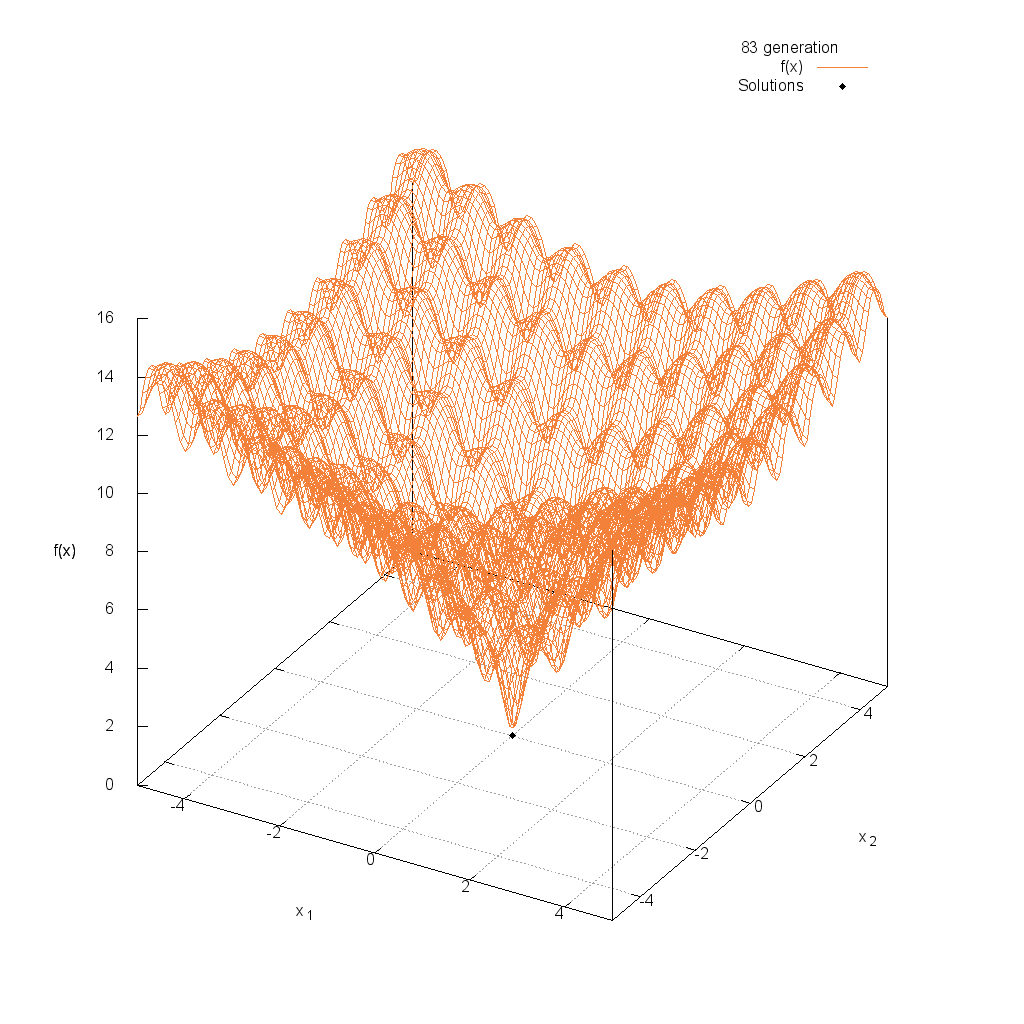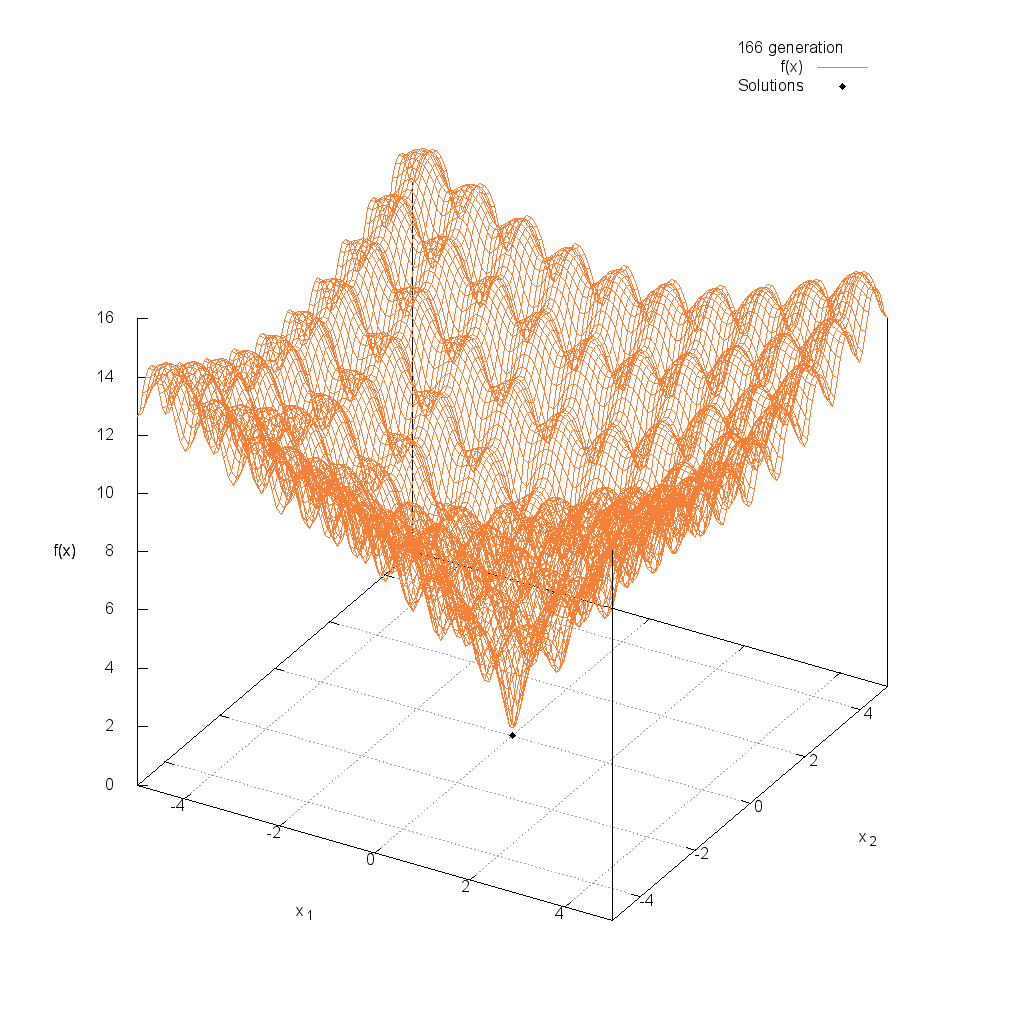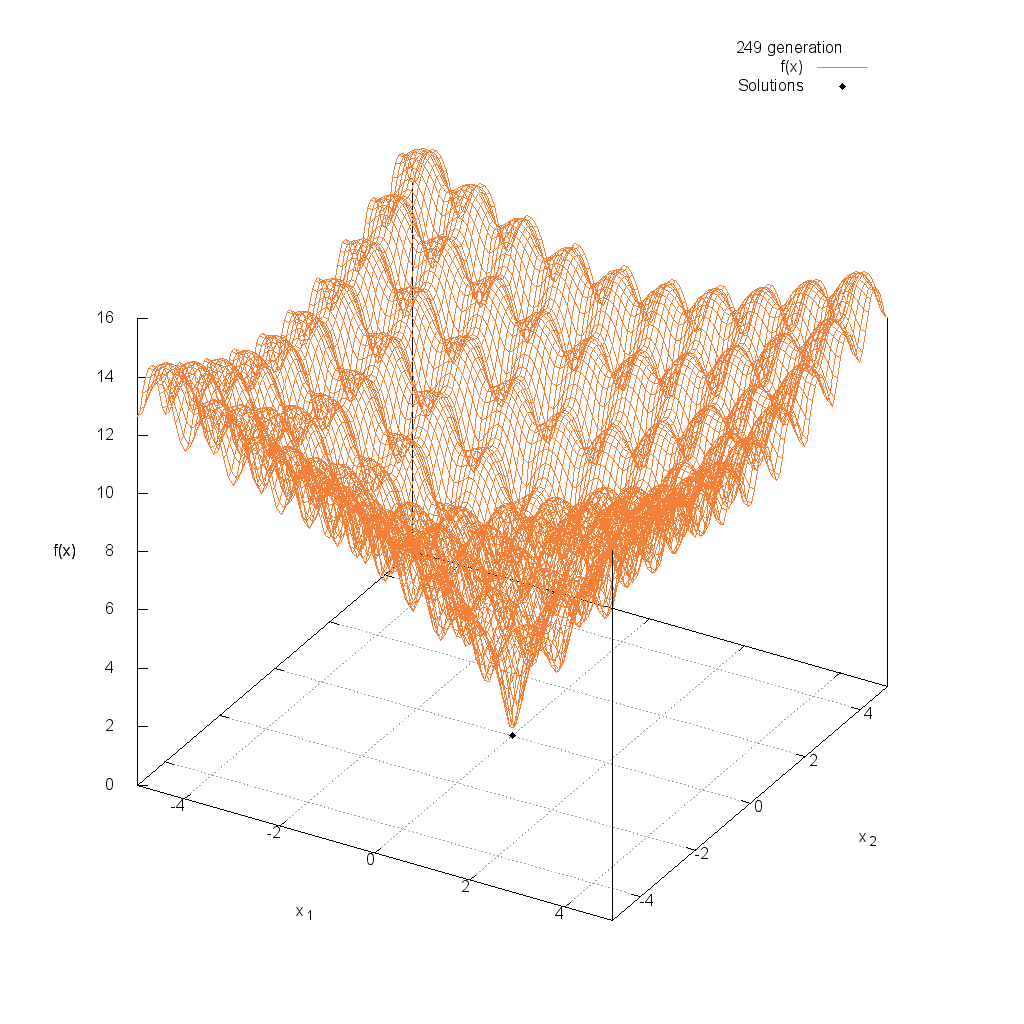
Three-hump関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = 2x_1^2-1.05x_1^4+\frac{x_1^6}{6}+x_1x_2+x_2^2$$
$$-2.0 \leq x_i \leq 2.0$$
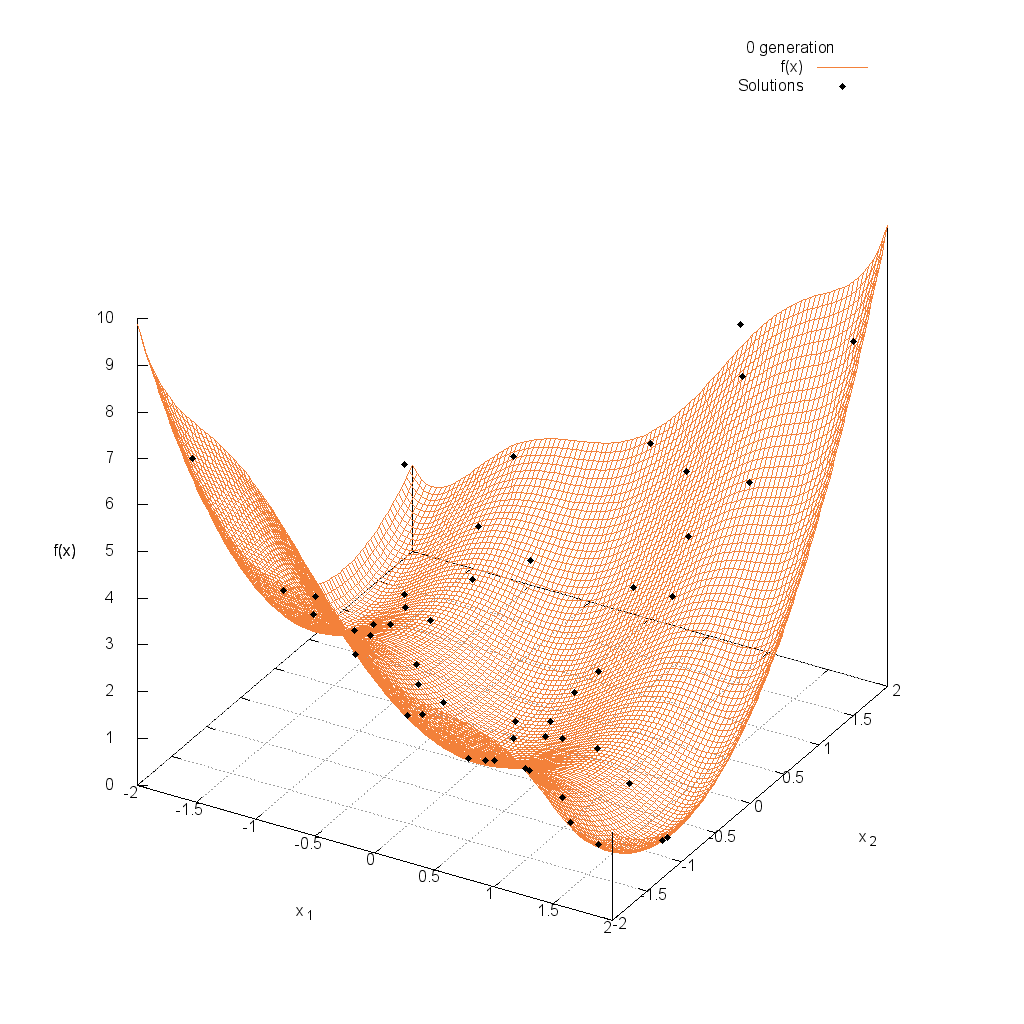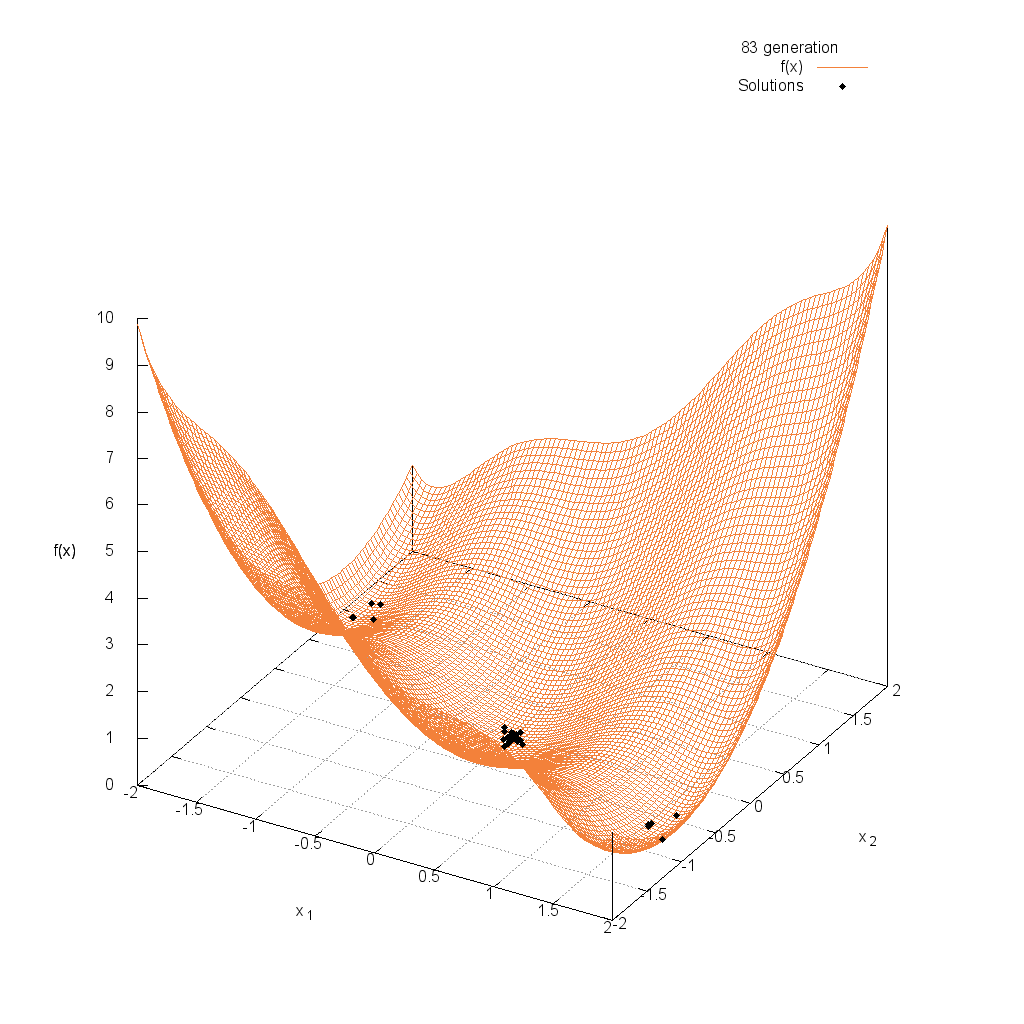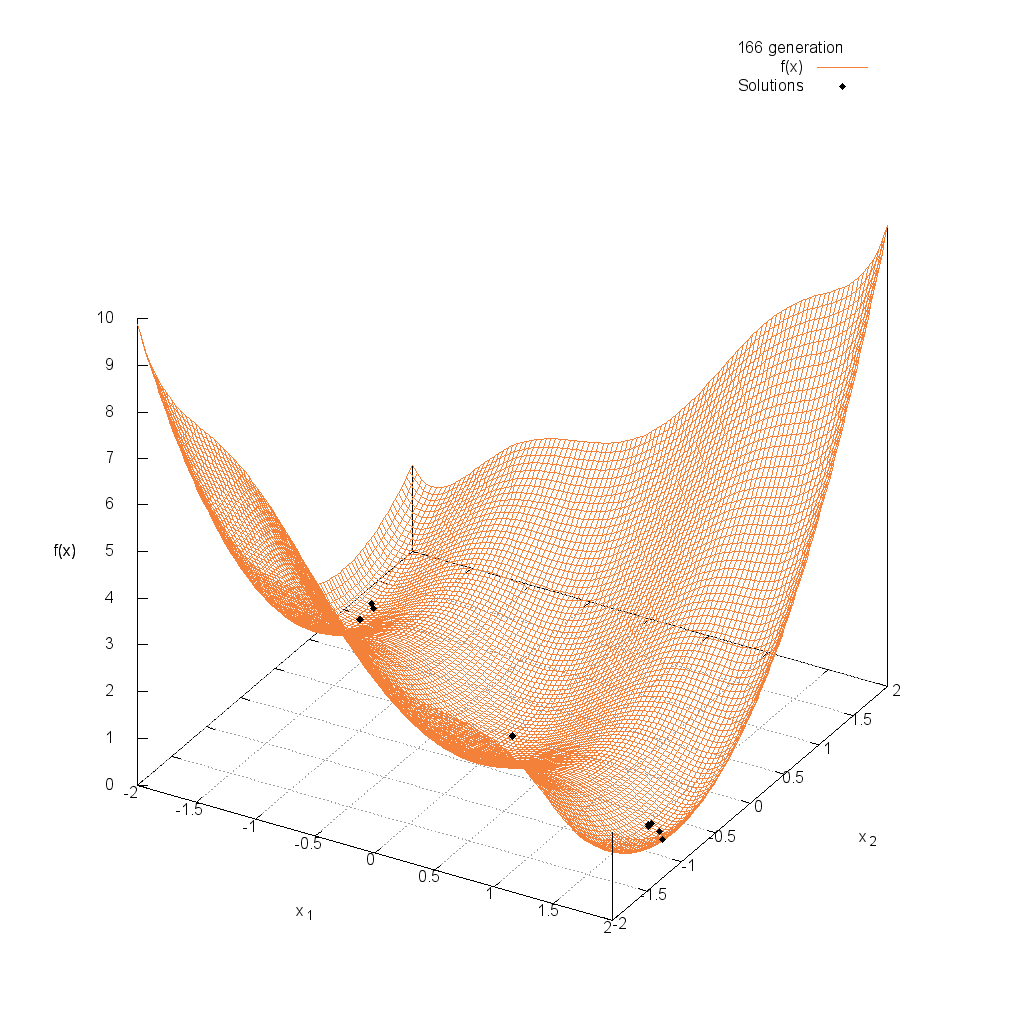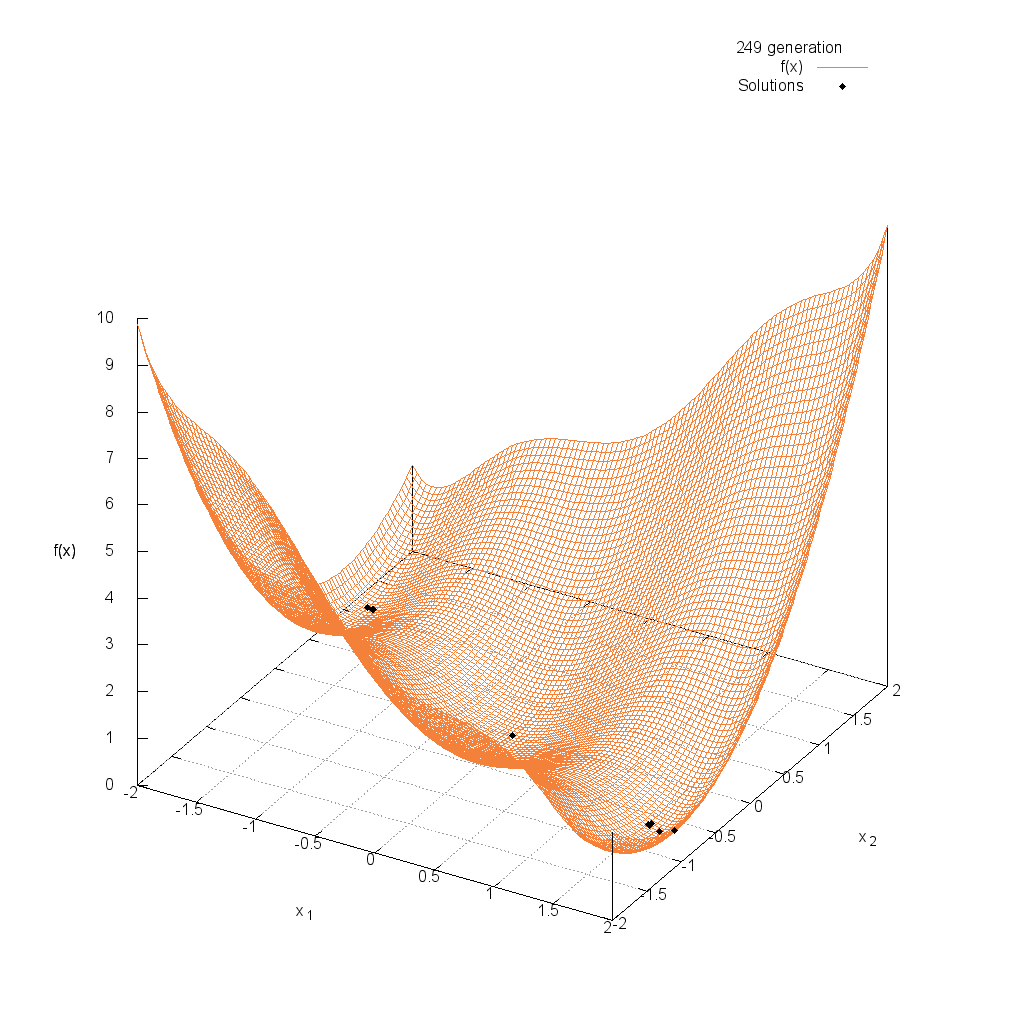
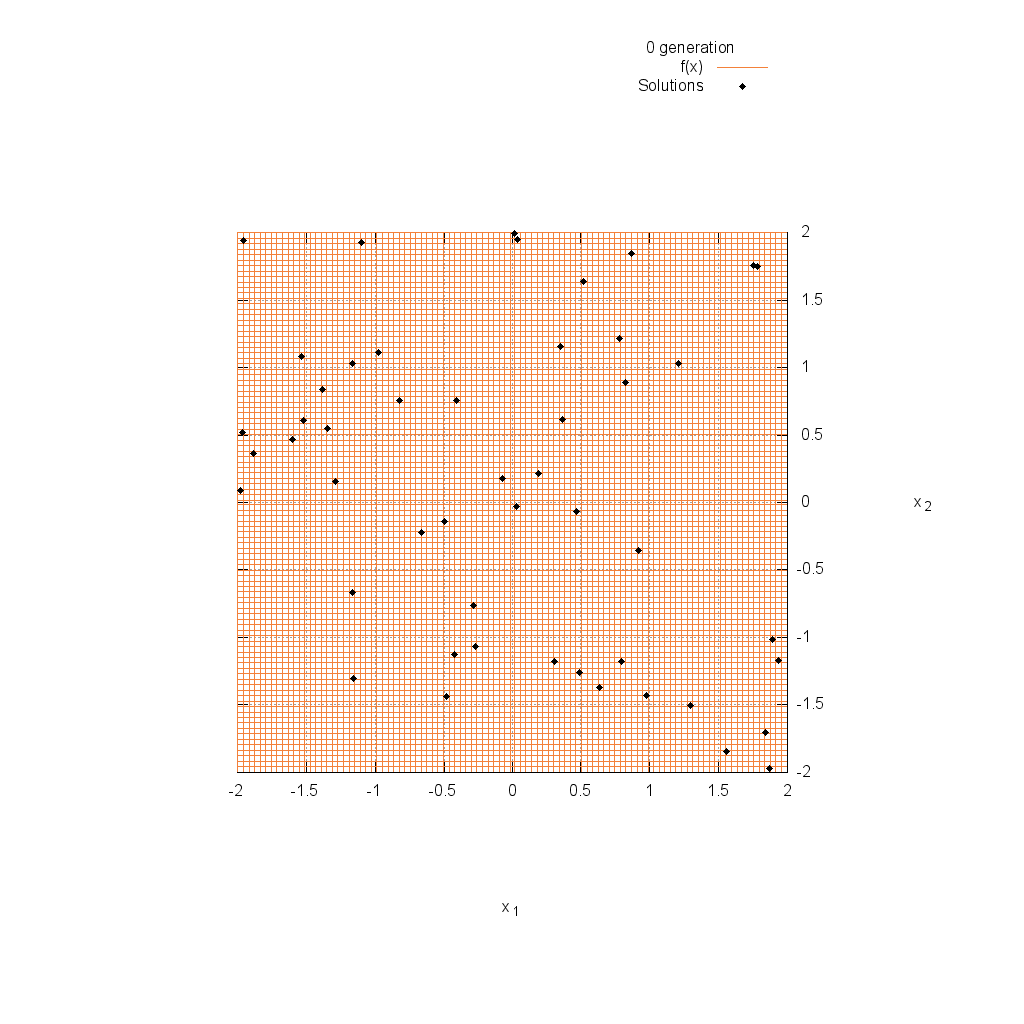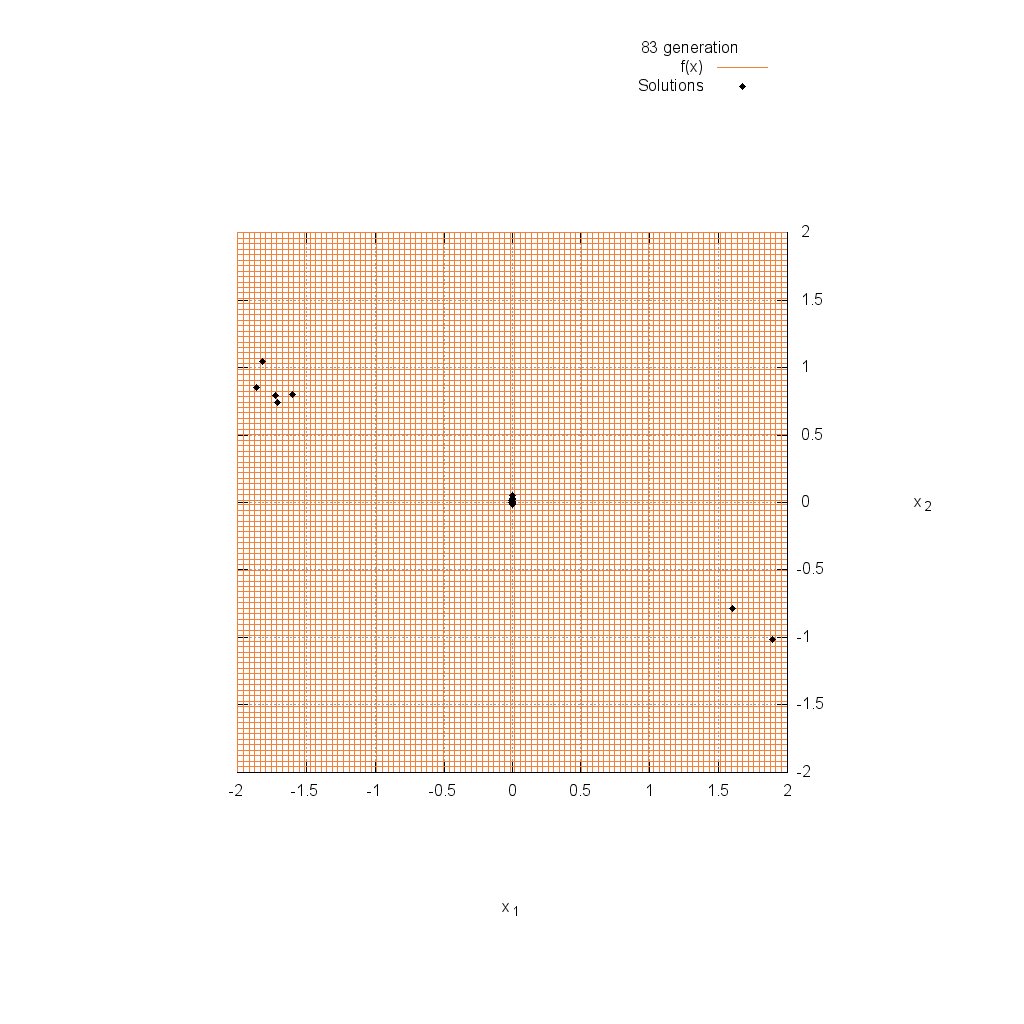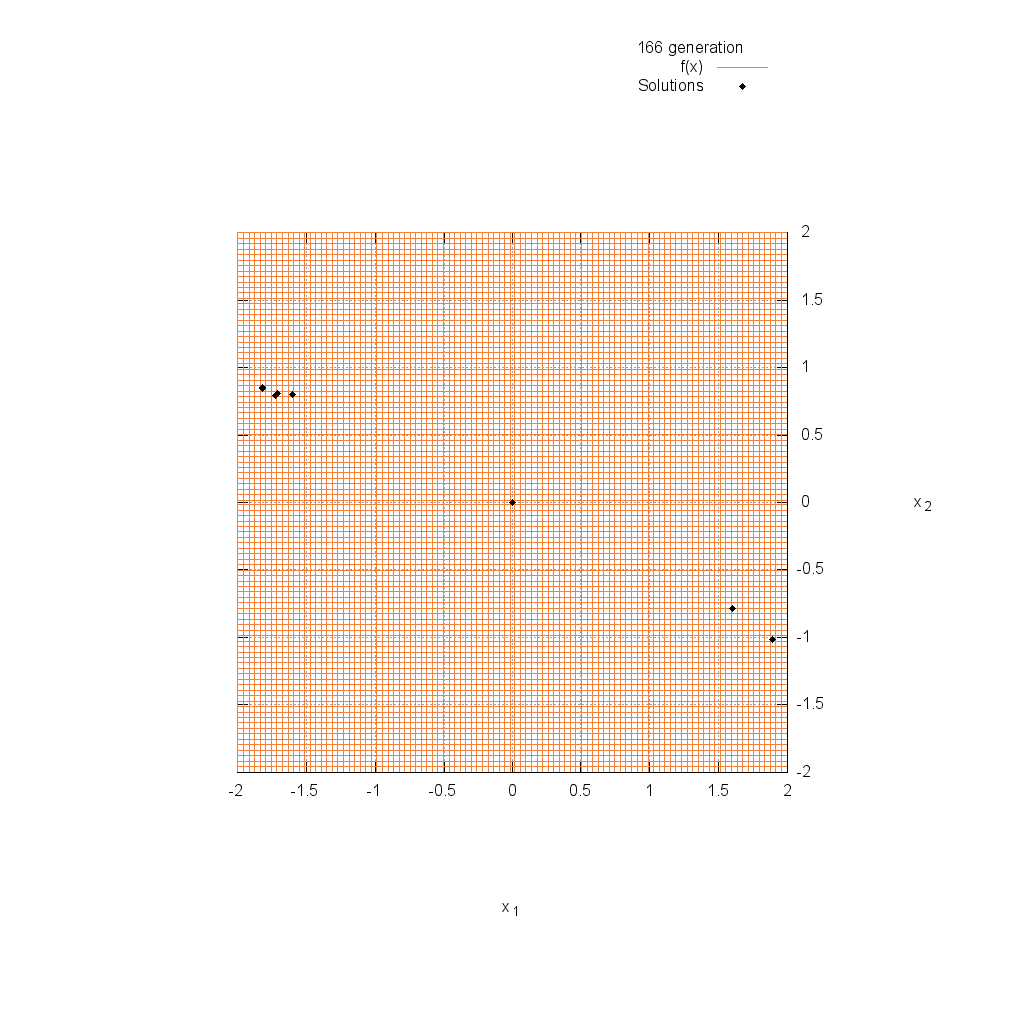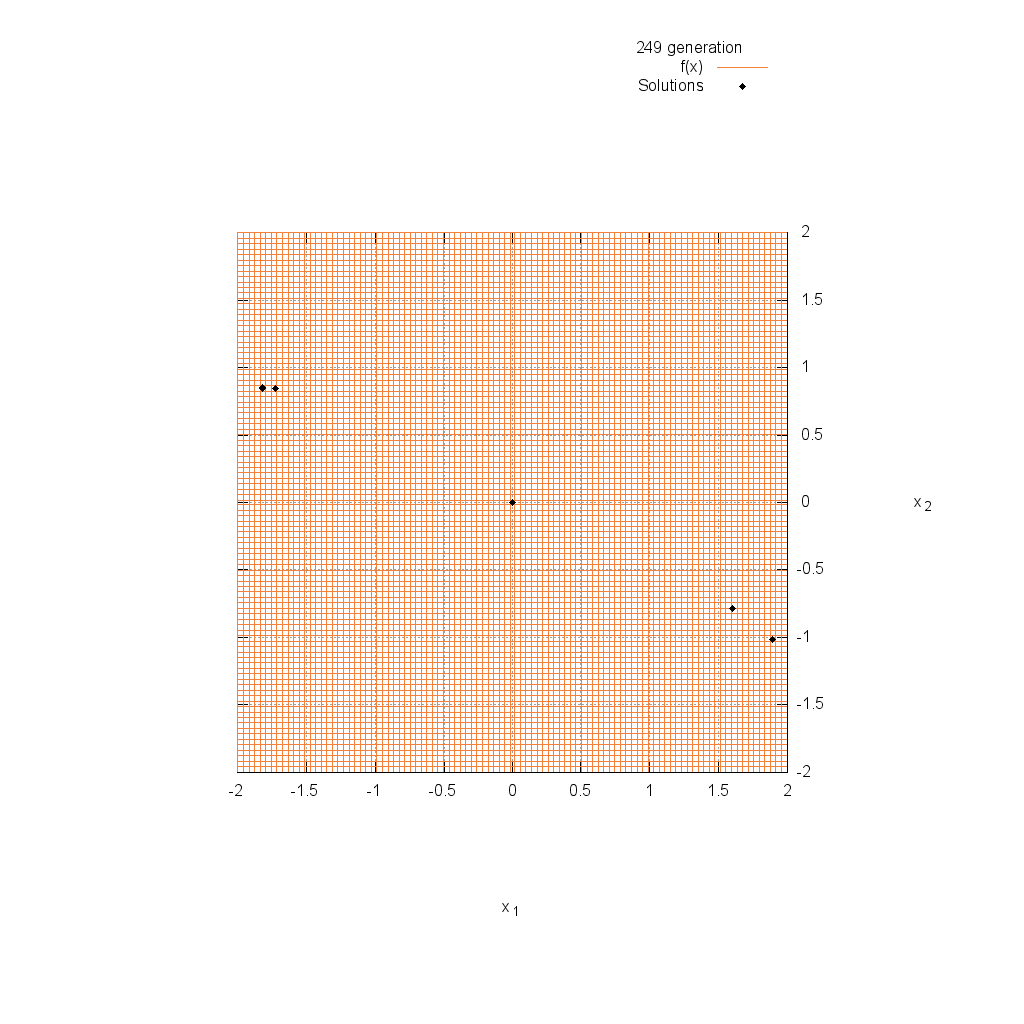
Easom関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = -\cos(x_1)\cos(x_2)\exp(-(x_1-\pi)^2-(x_2-\pi)^2)$$
$$-5.0 \leq x_i \leq 5.0$$
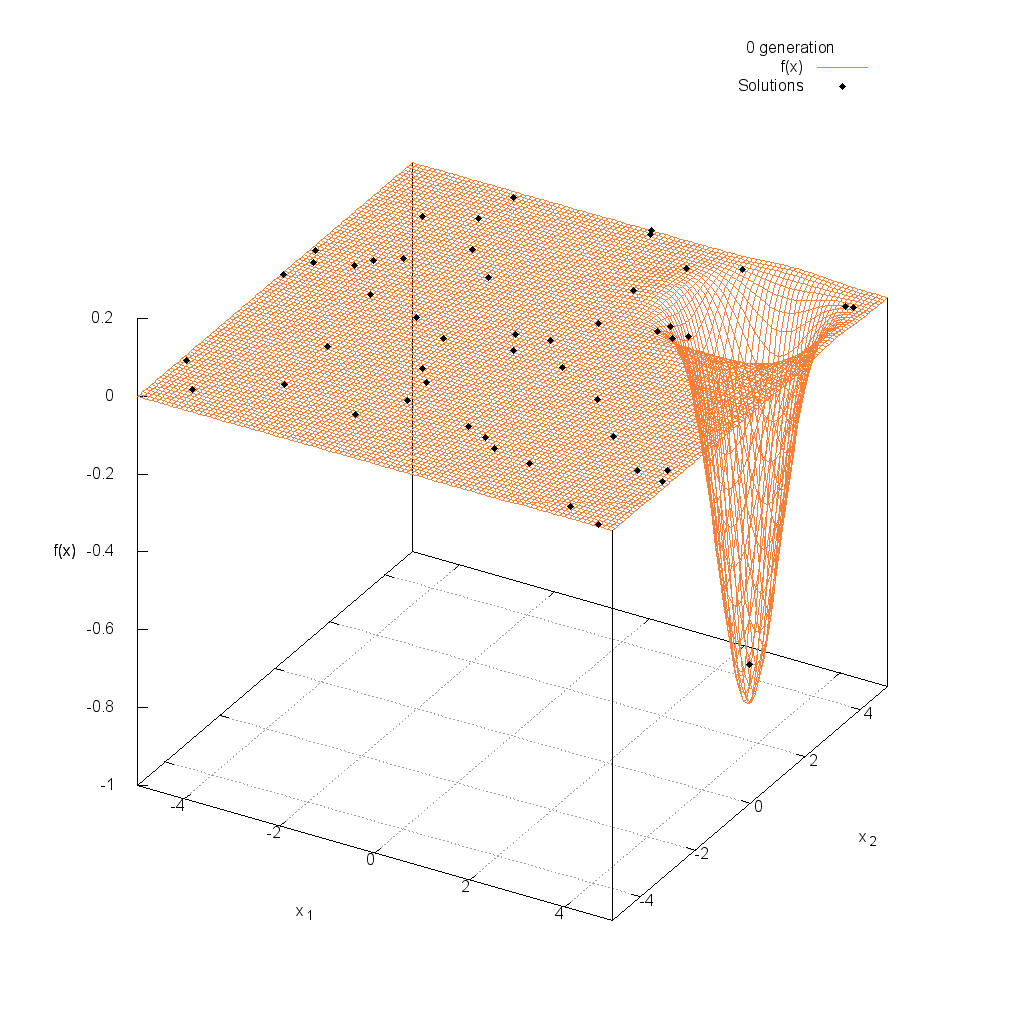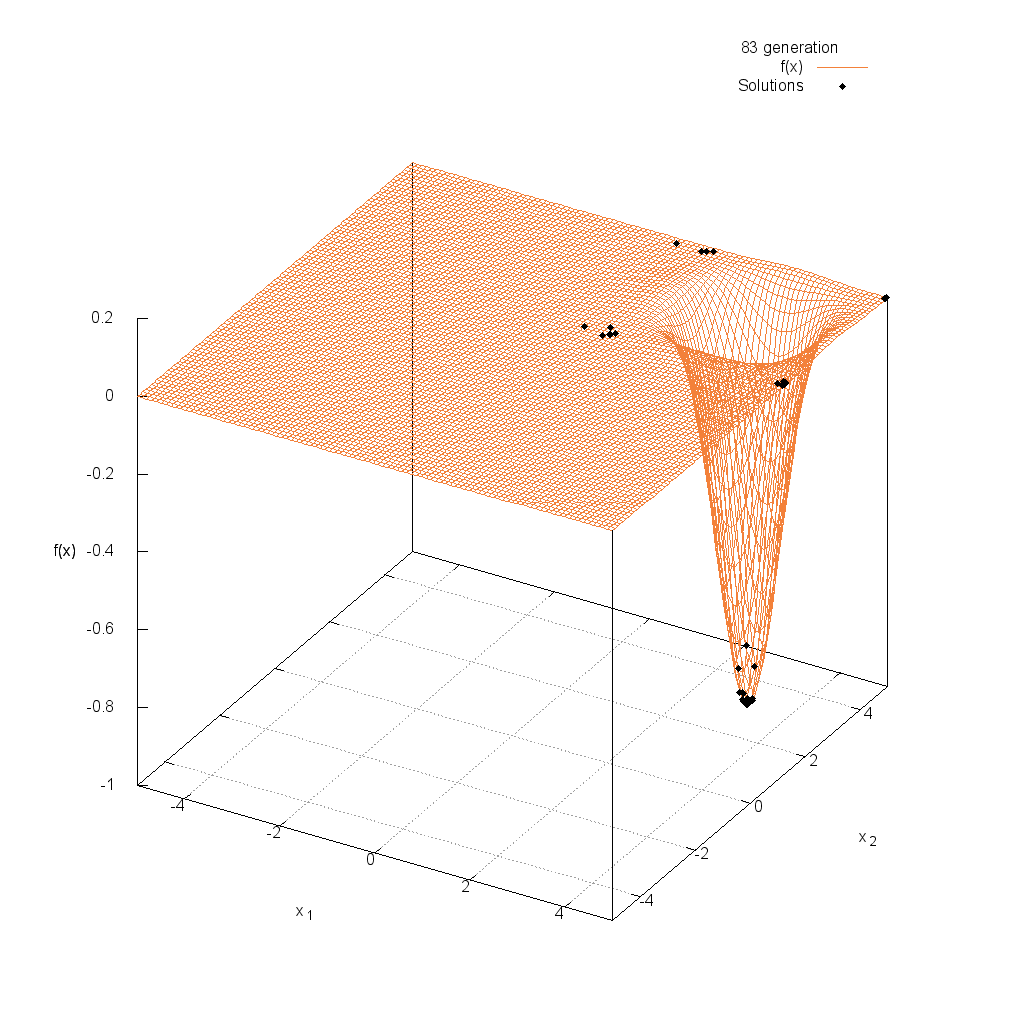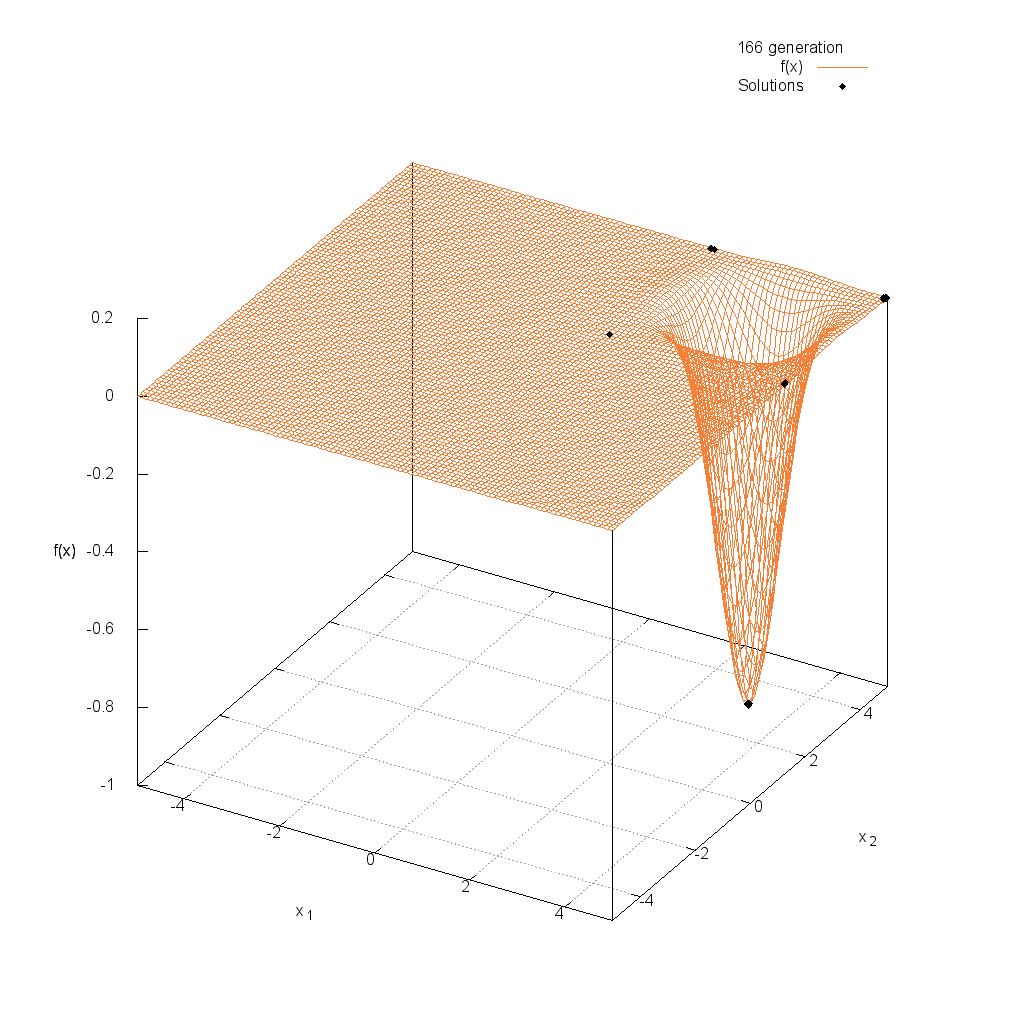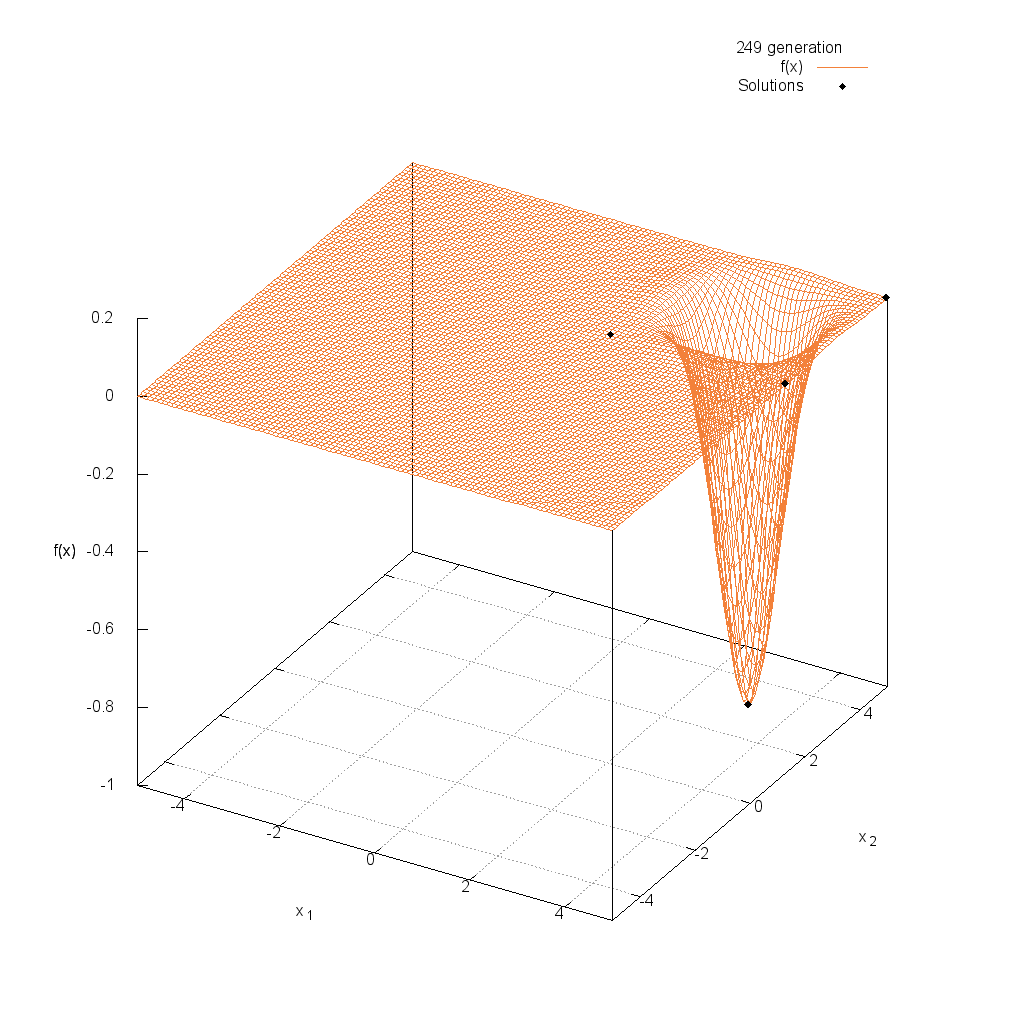
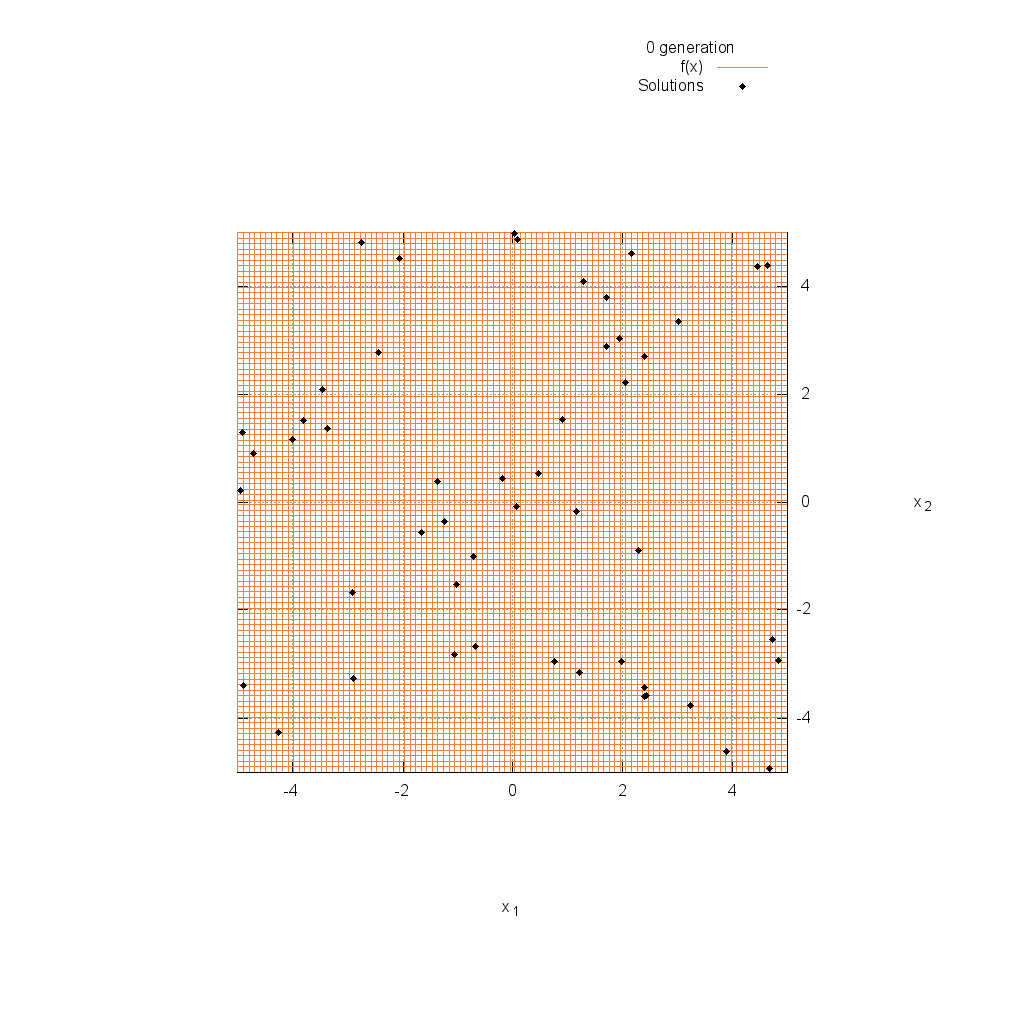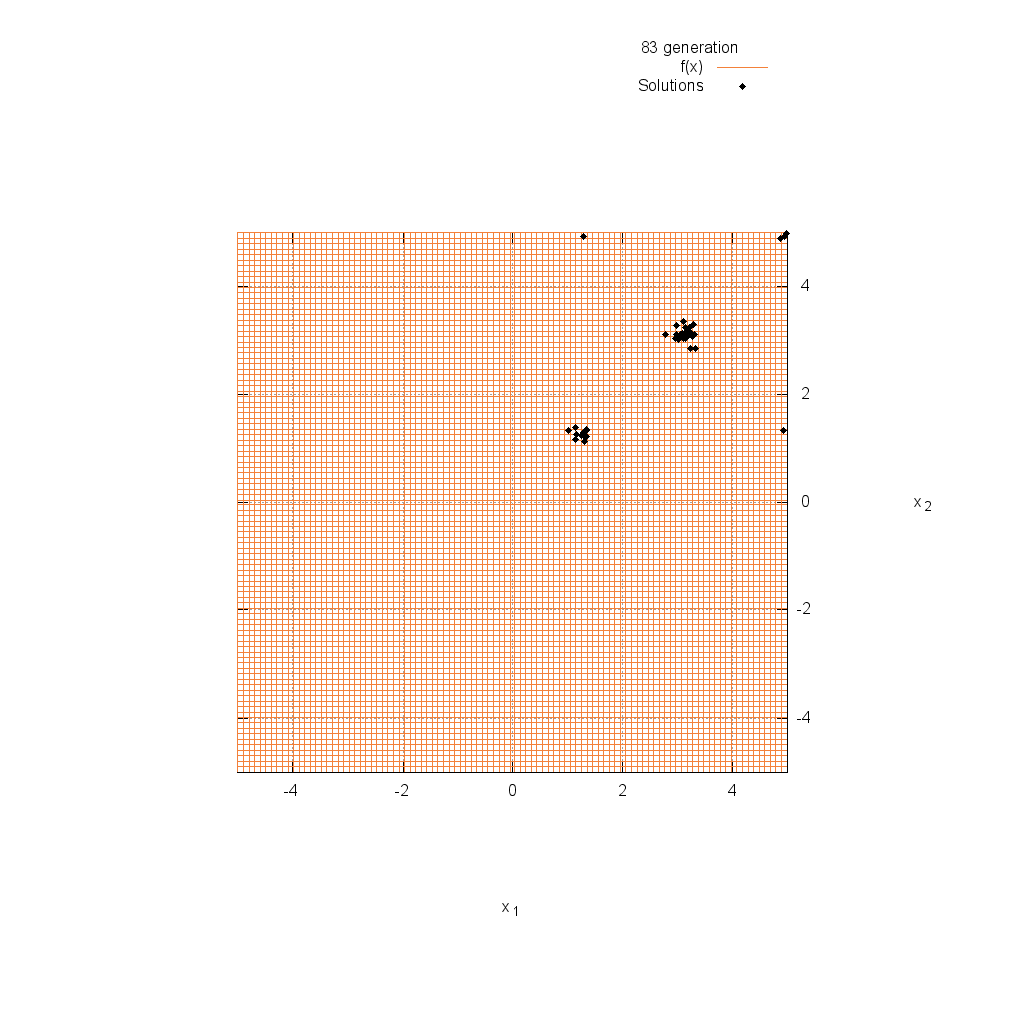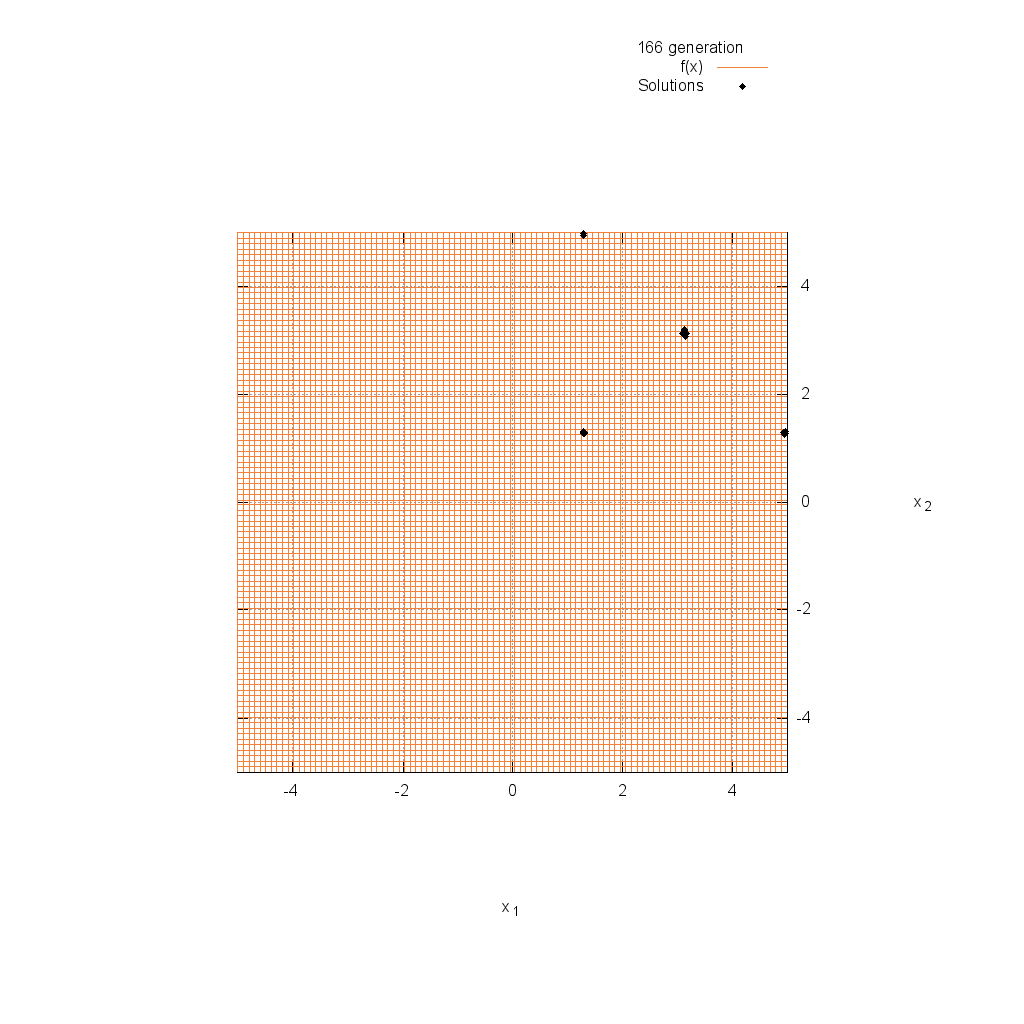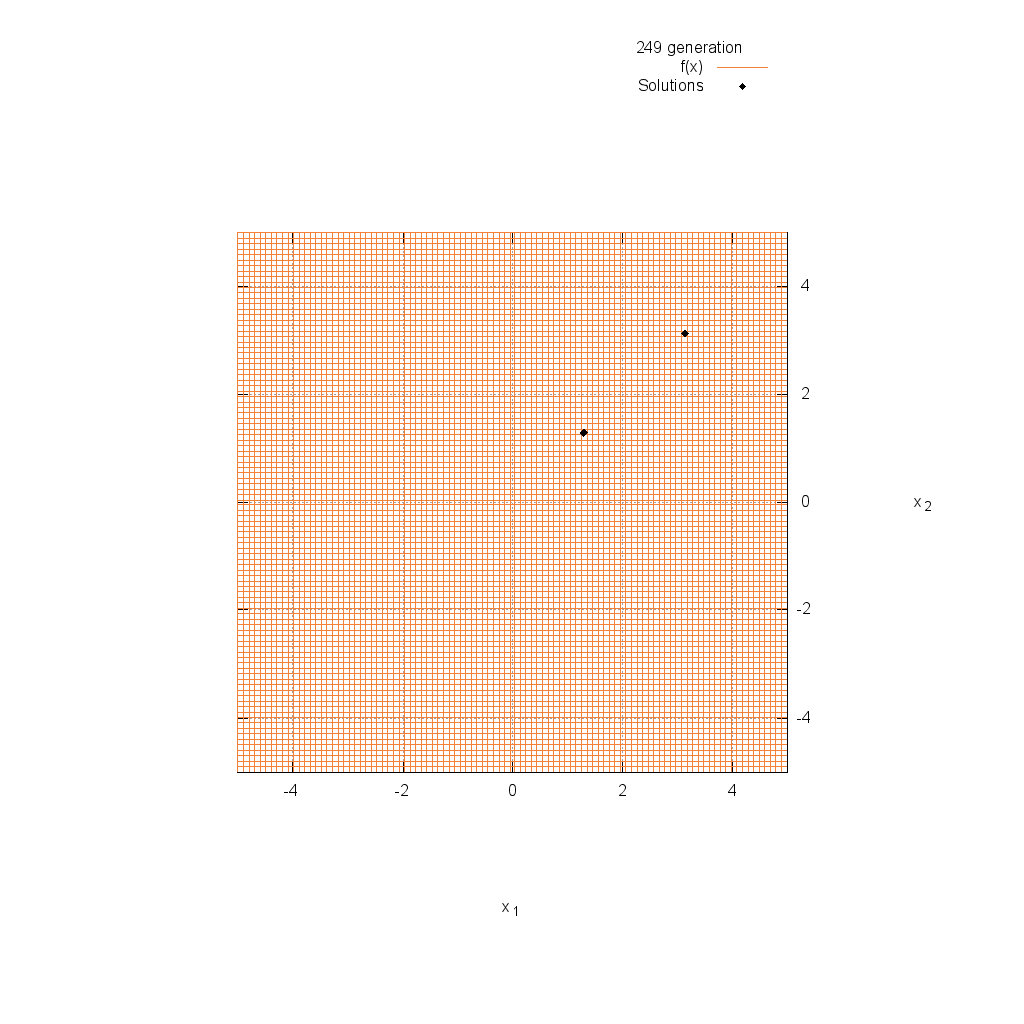
Griewank関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = 1 + \frac{1}{4000} \sum_{i=1}^n x^2_i – \prod_{i=1}^n \cos(\frac{x_i}{\sqrt{i}})$$
$$-5.0 \leq x_i \leq 5.0$$
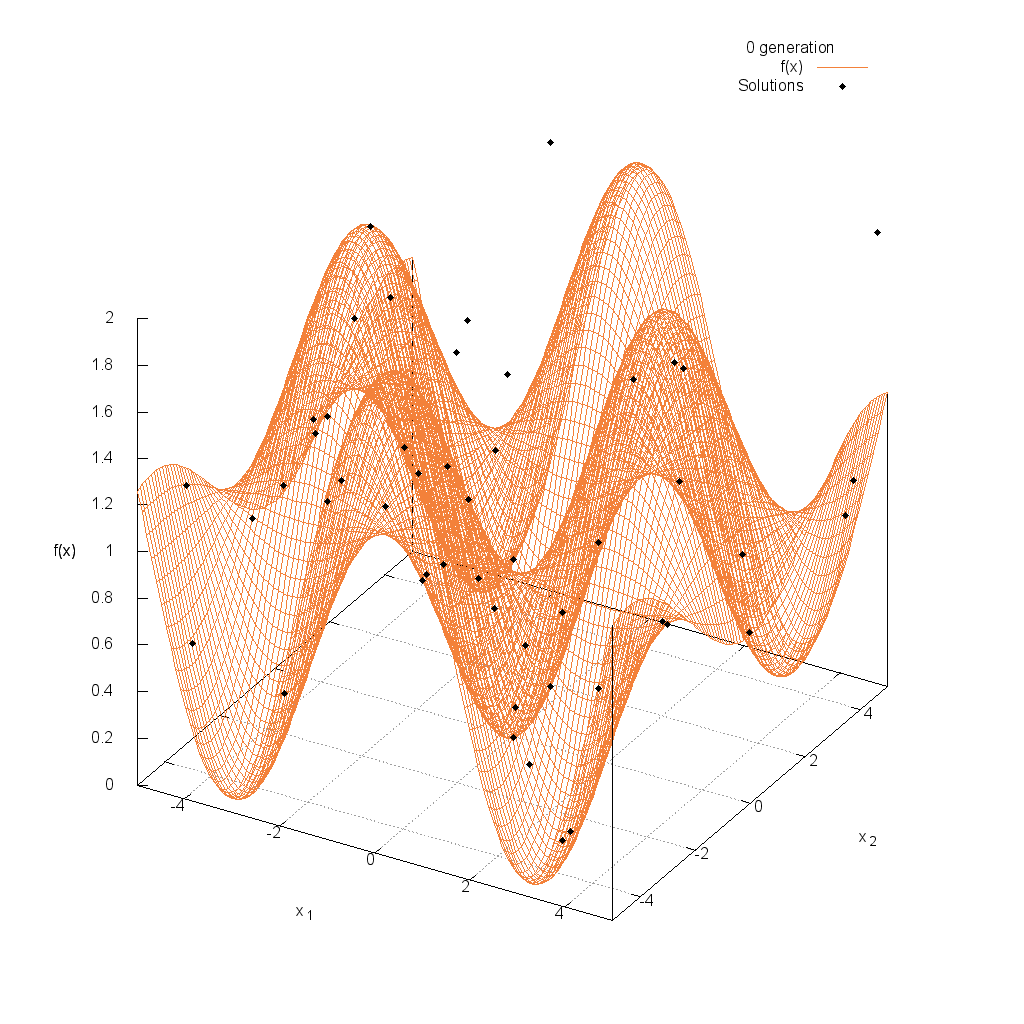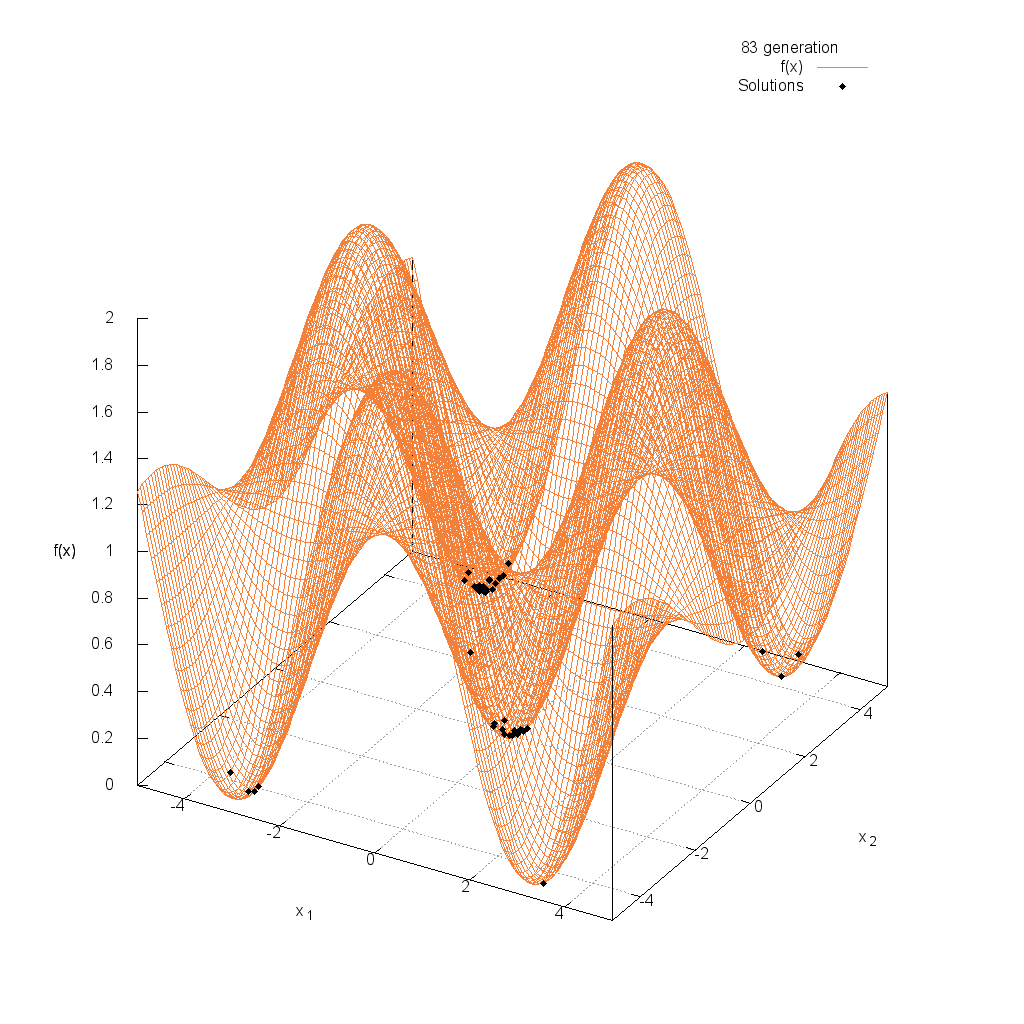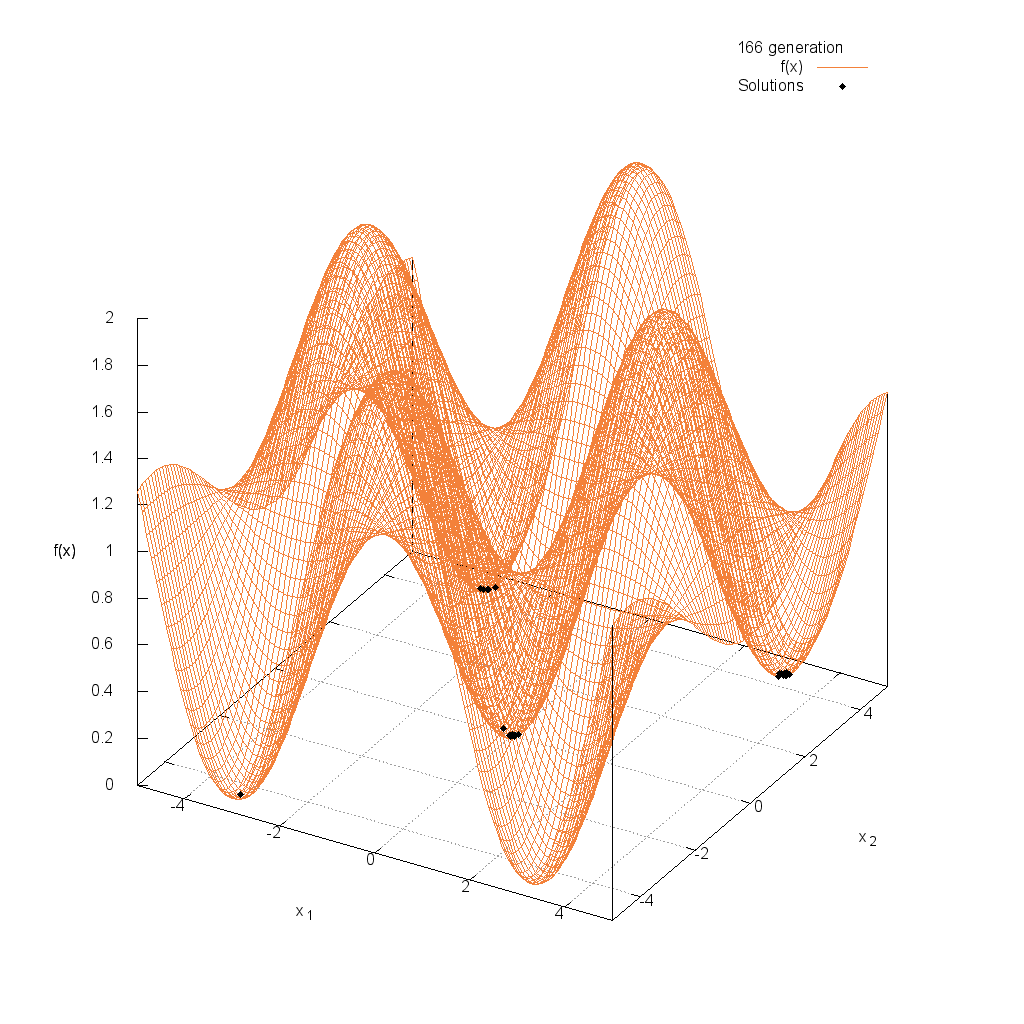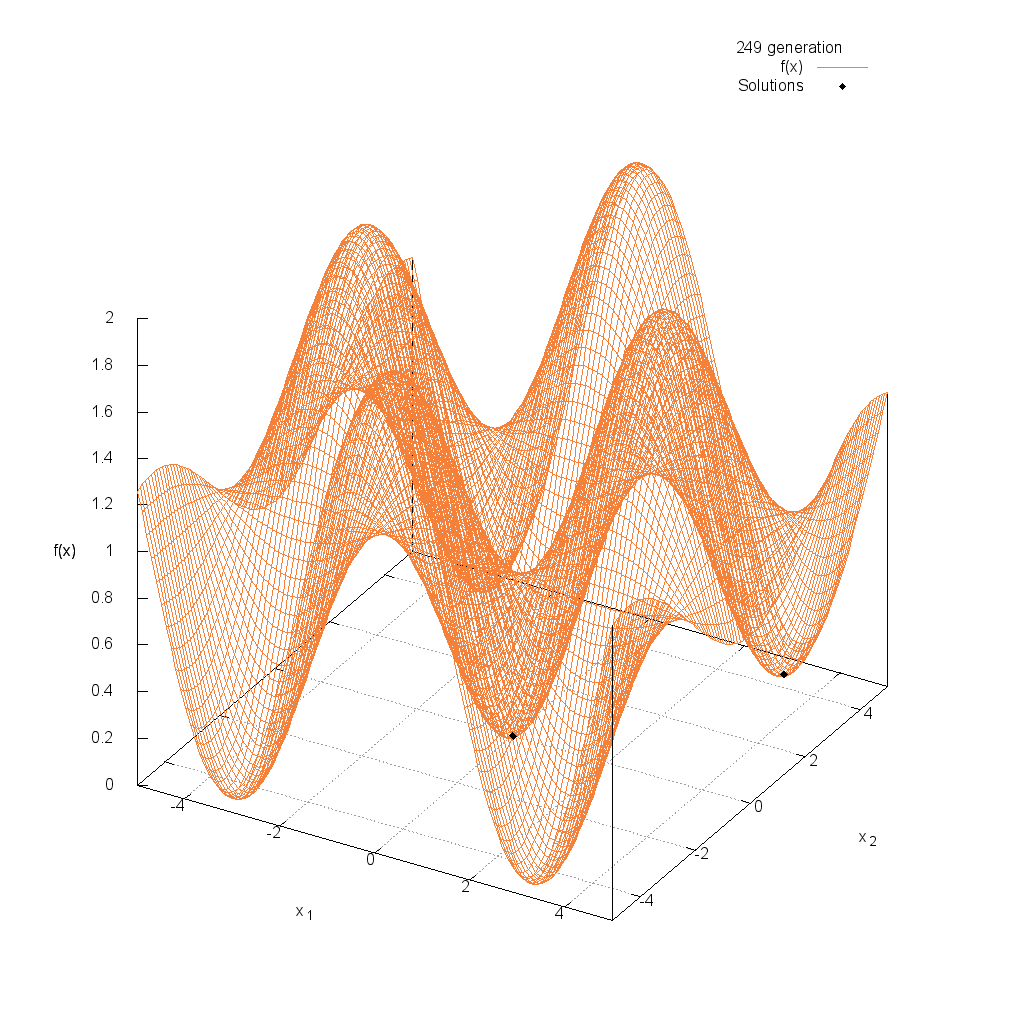
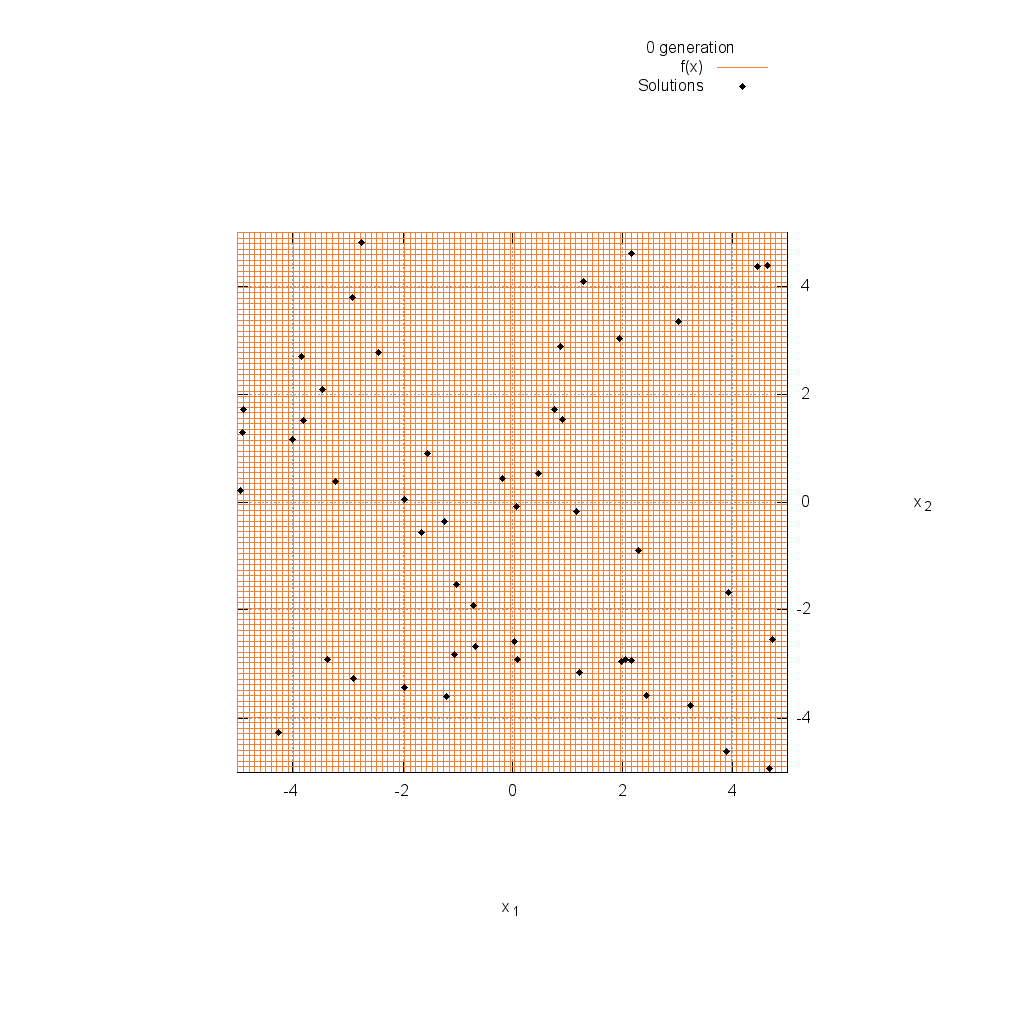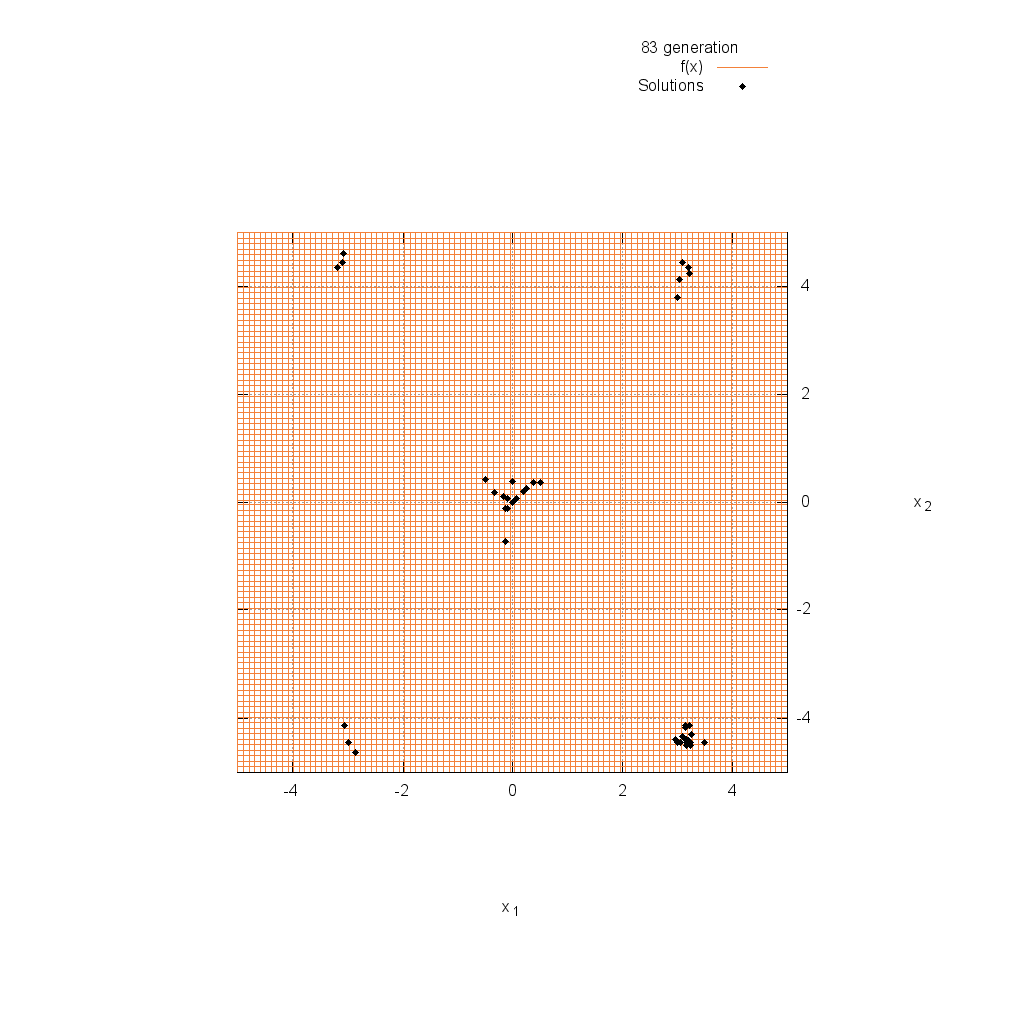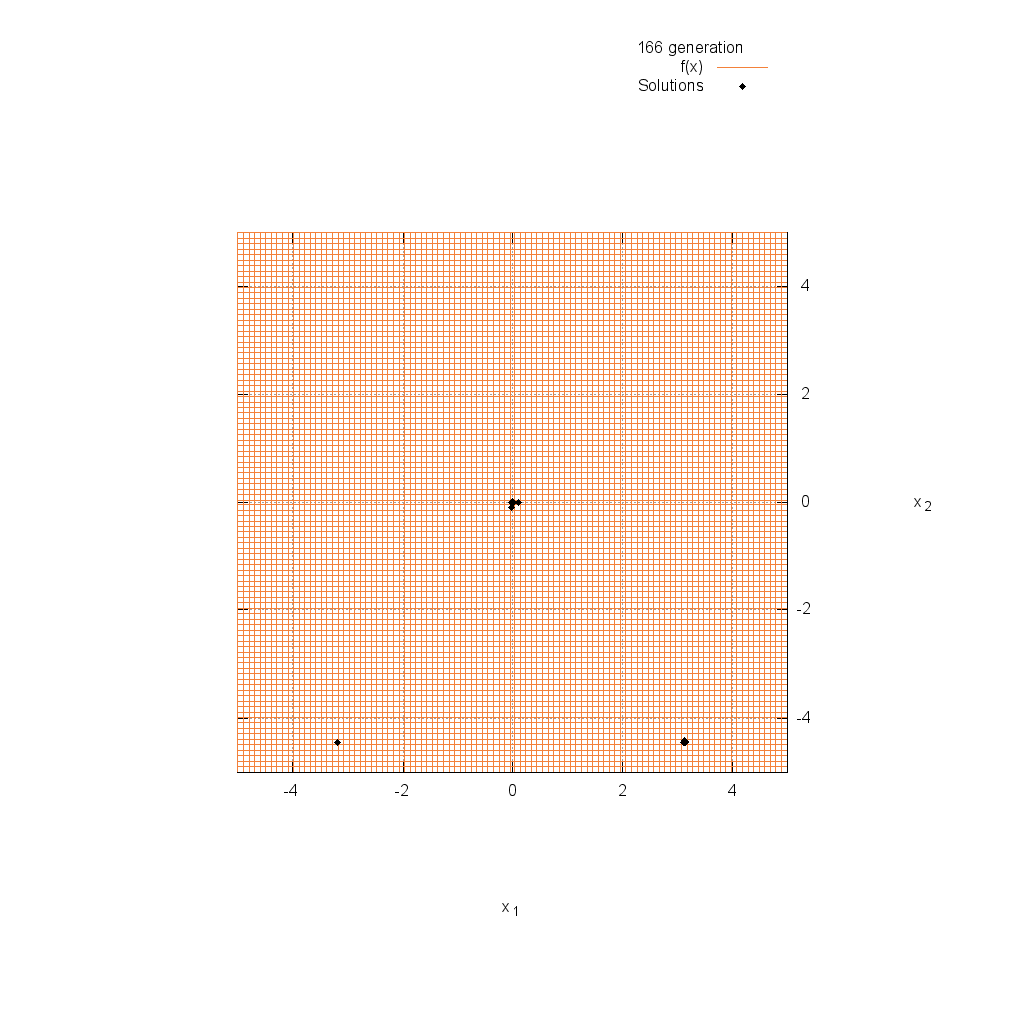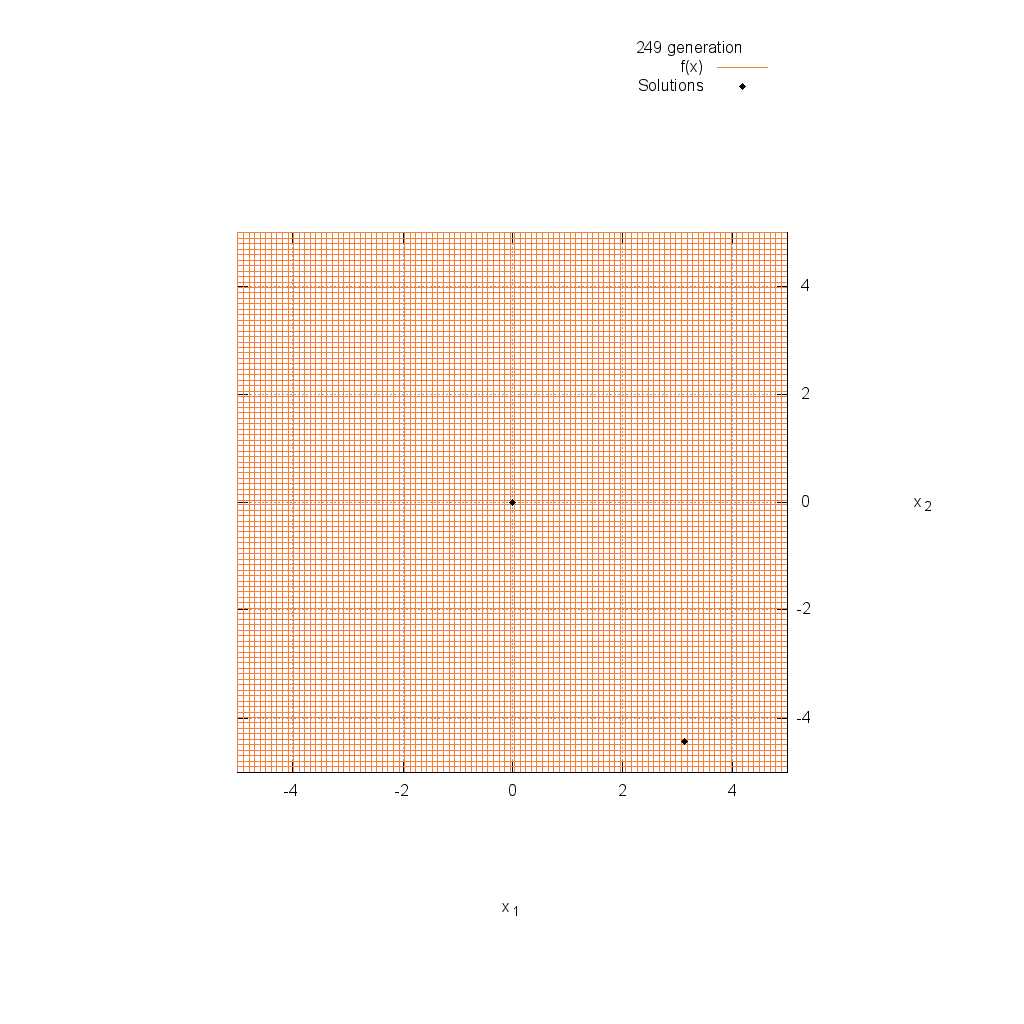
Michalewicz関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = -\sum_{i=1}^{n}\sin(x_i)\sin^{20}(\frac{ix_i^2}{\pi})$$
$$\pi \leq x_i \leq \pi$$
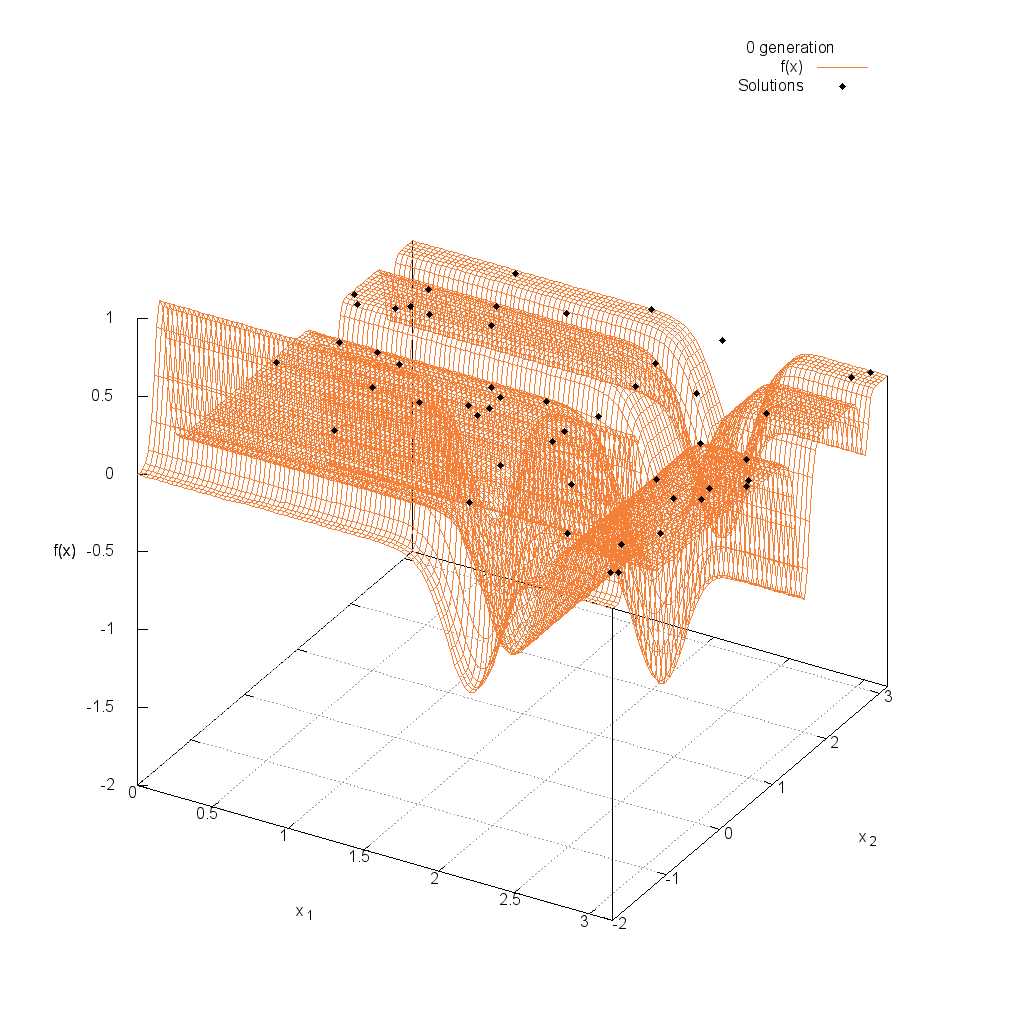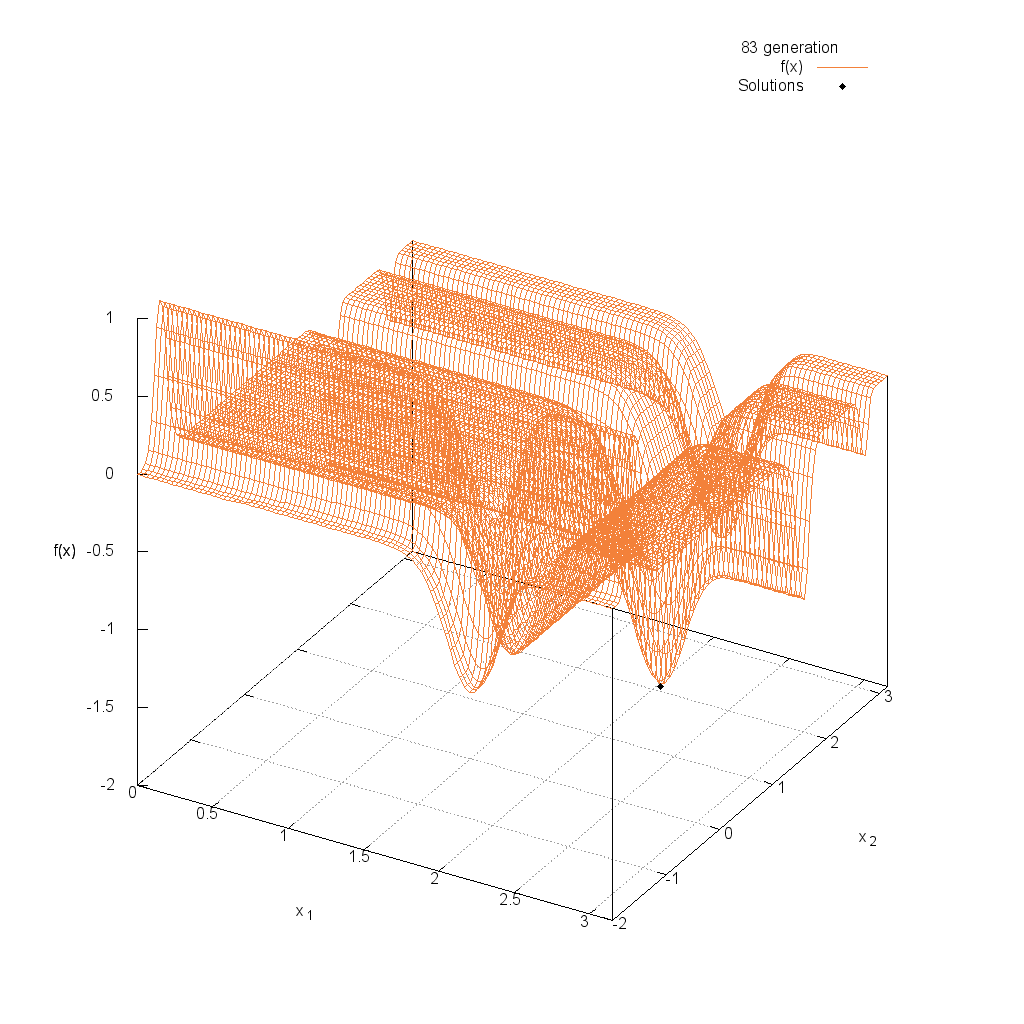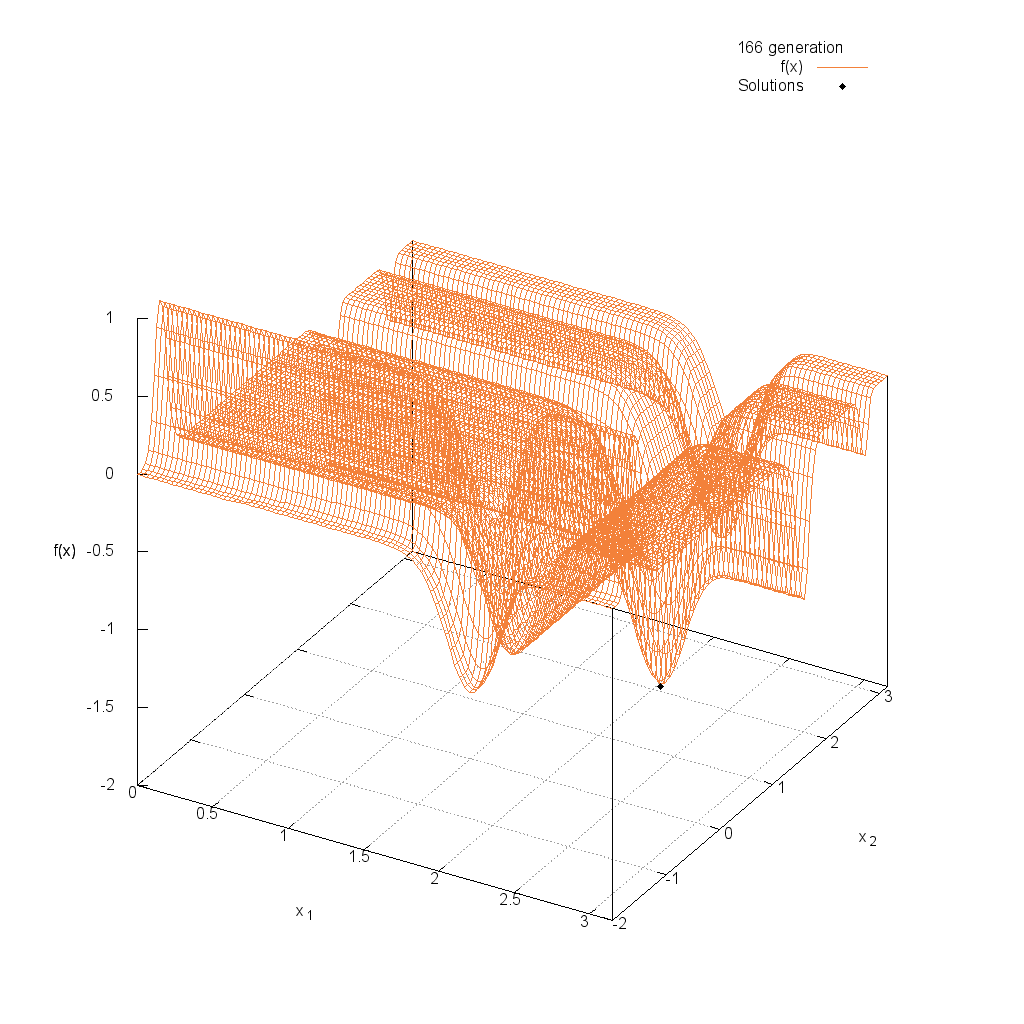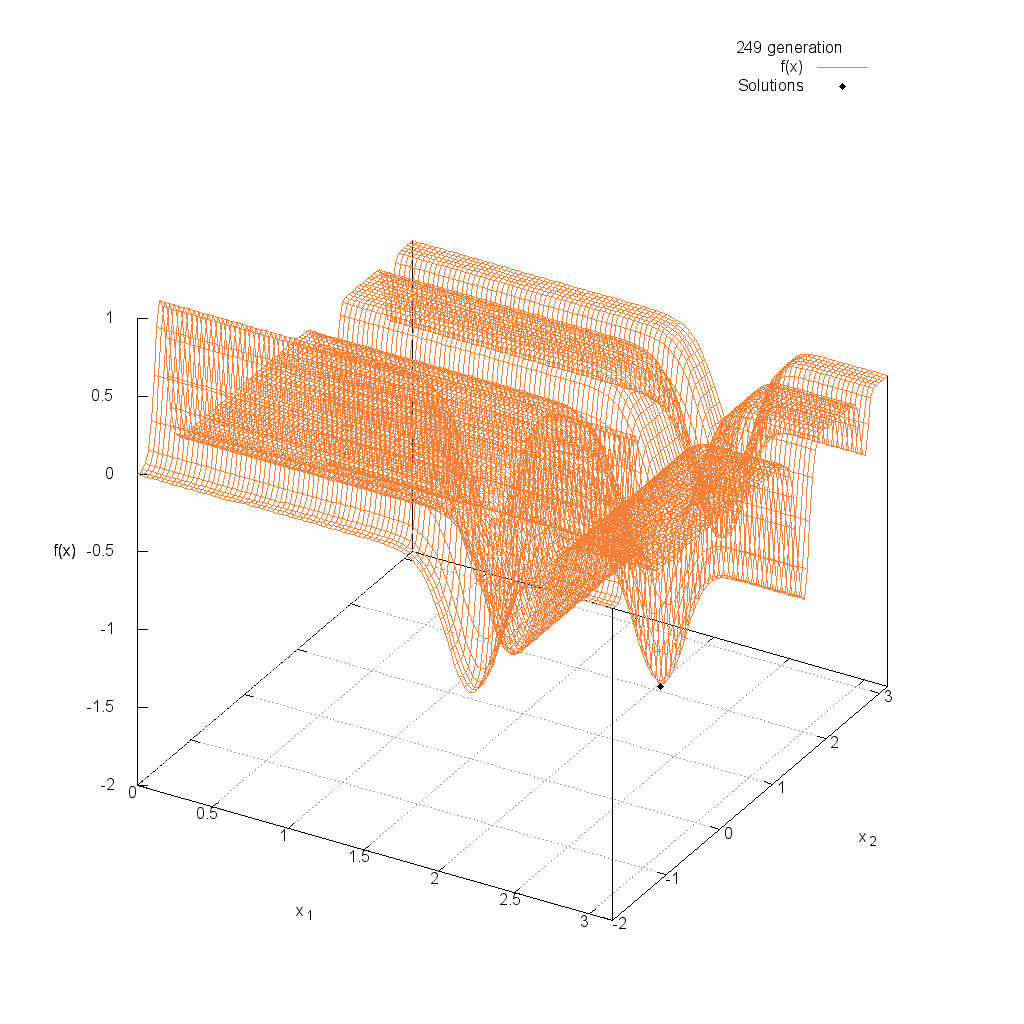
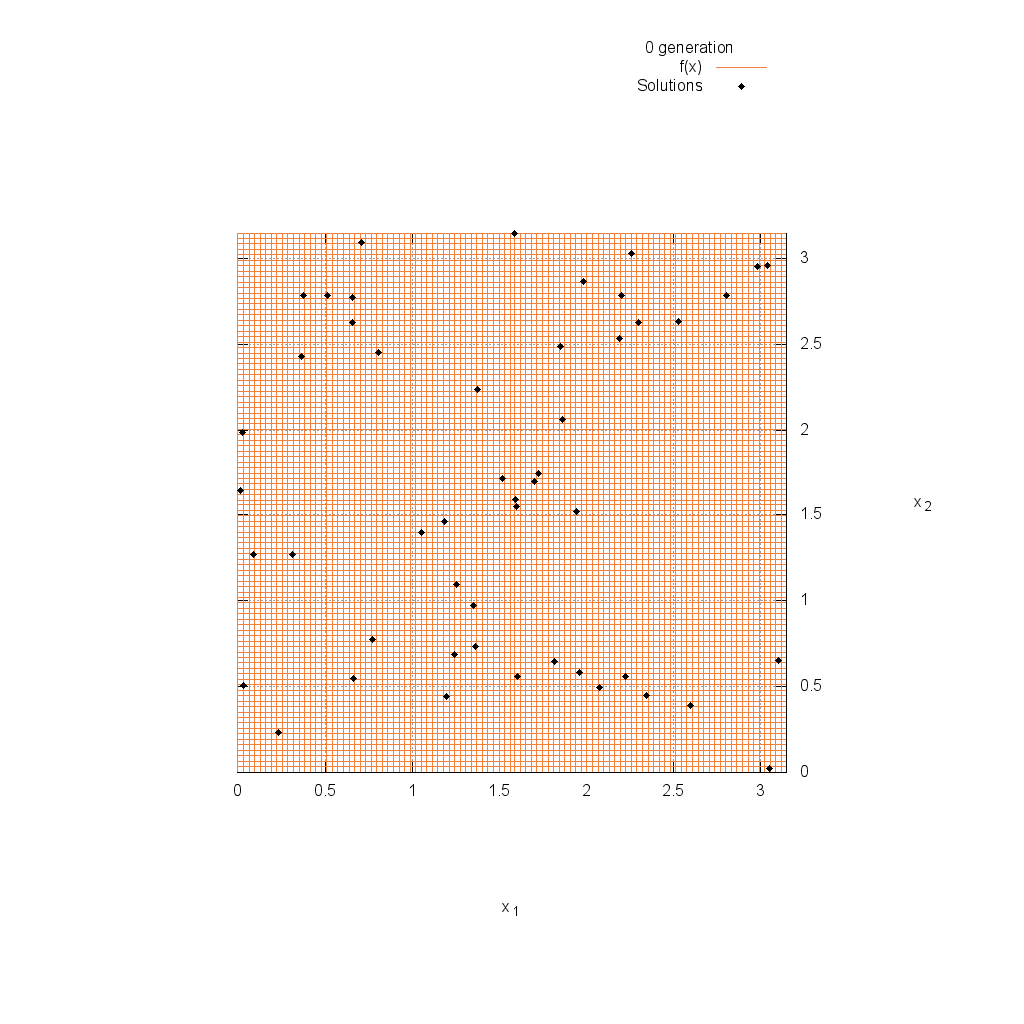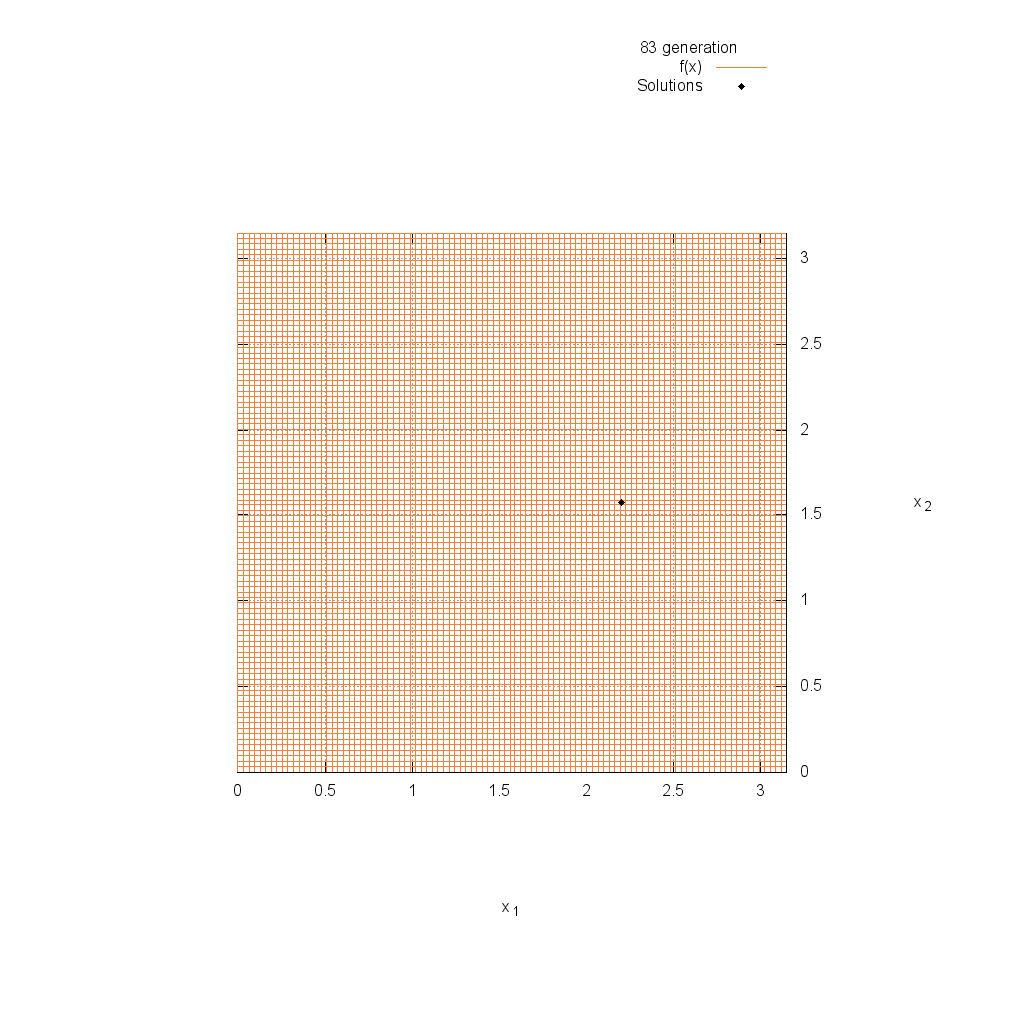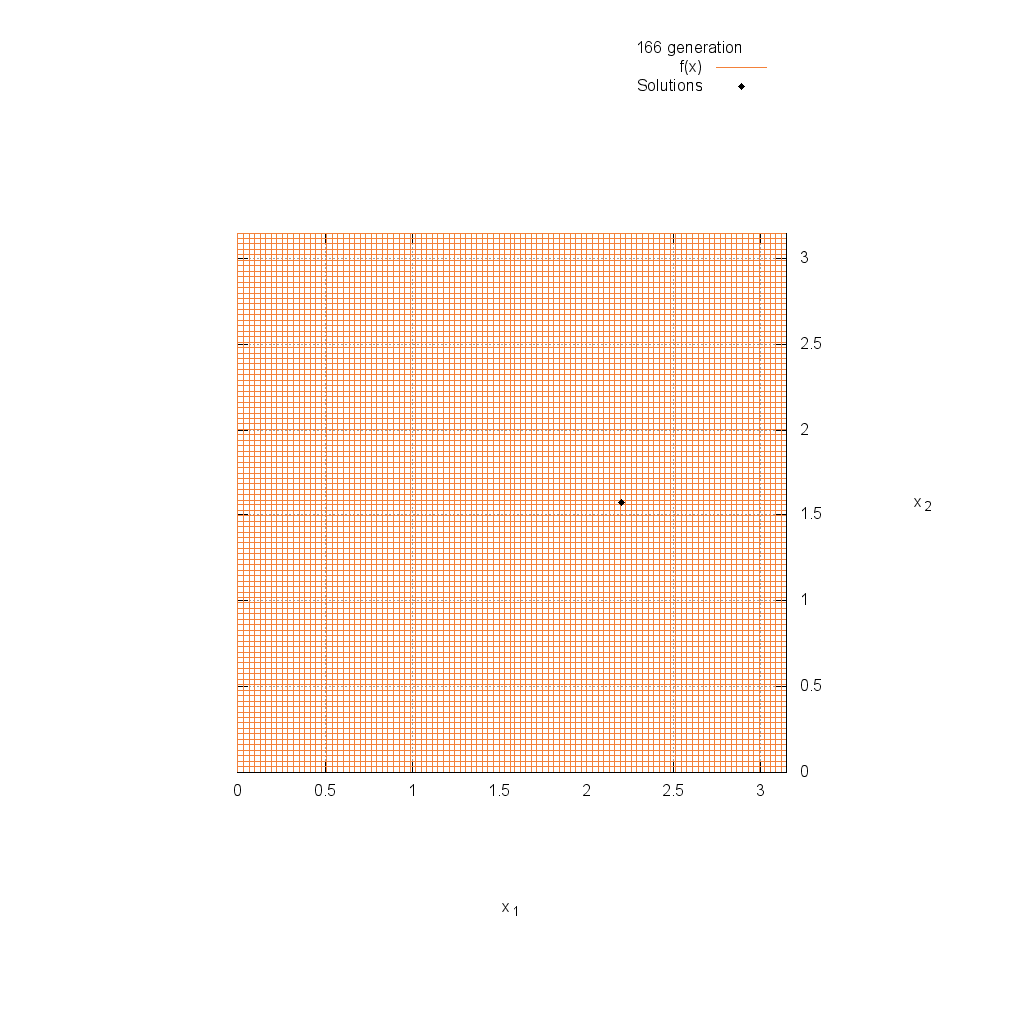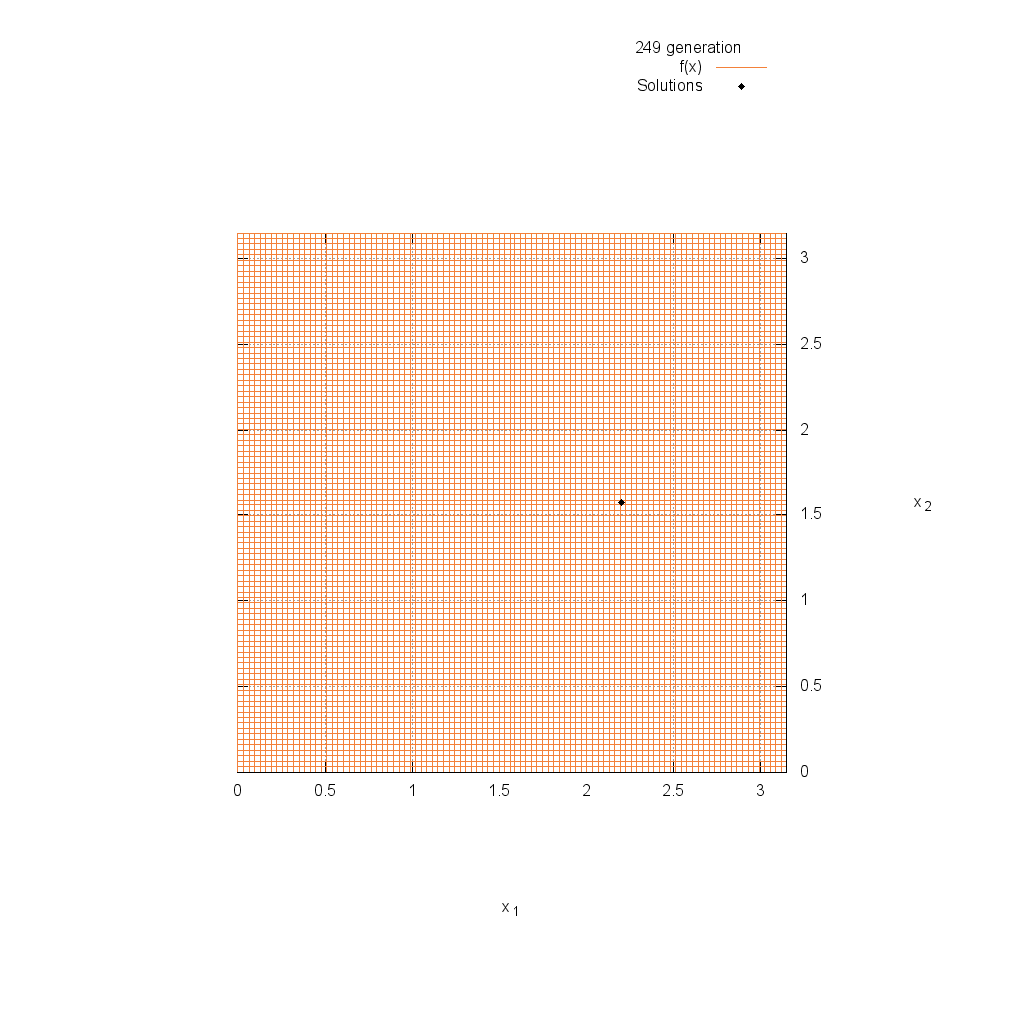
Rastrigin関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = 10n + \sum_{i=1}^n (x_i^2 -10\cos(2\pi x_i))$$
$$5.12 \leq x_i \leq 5.12$$
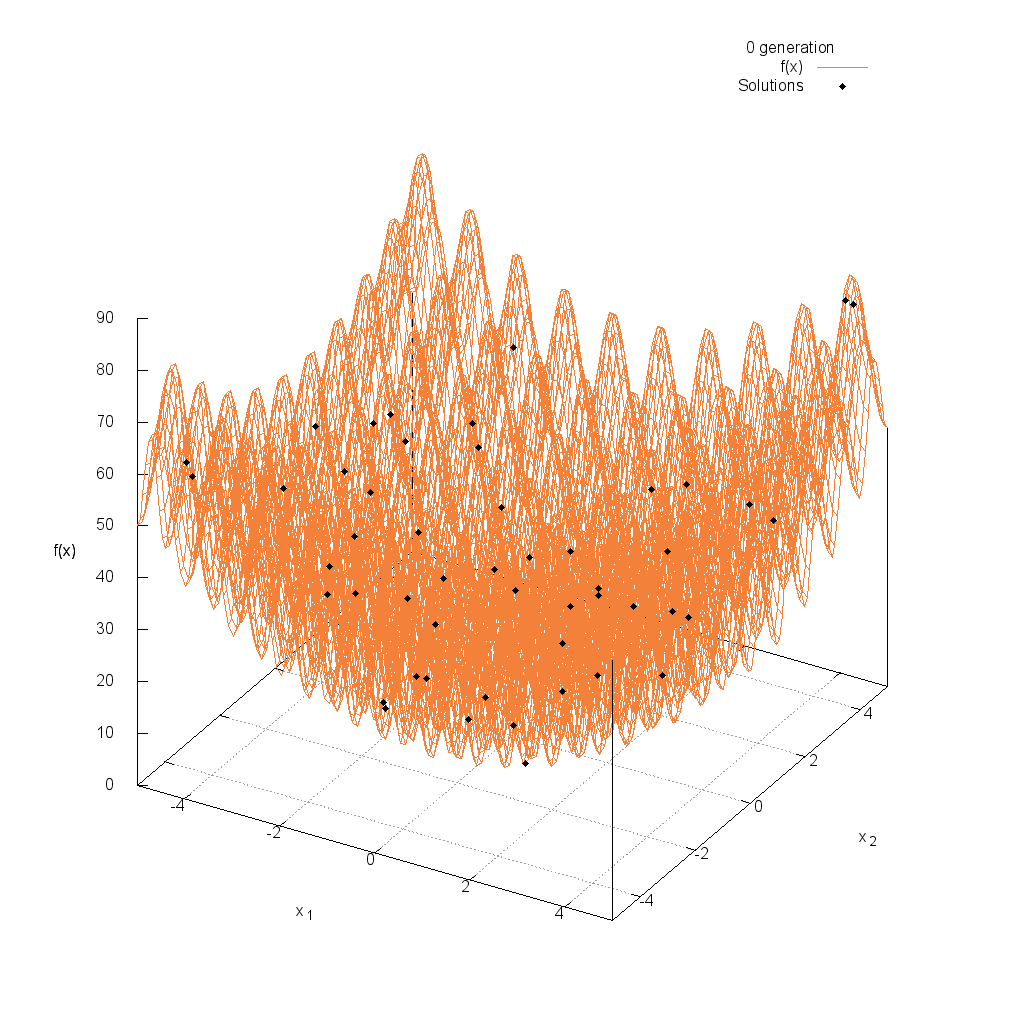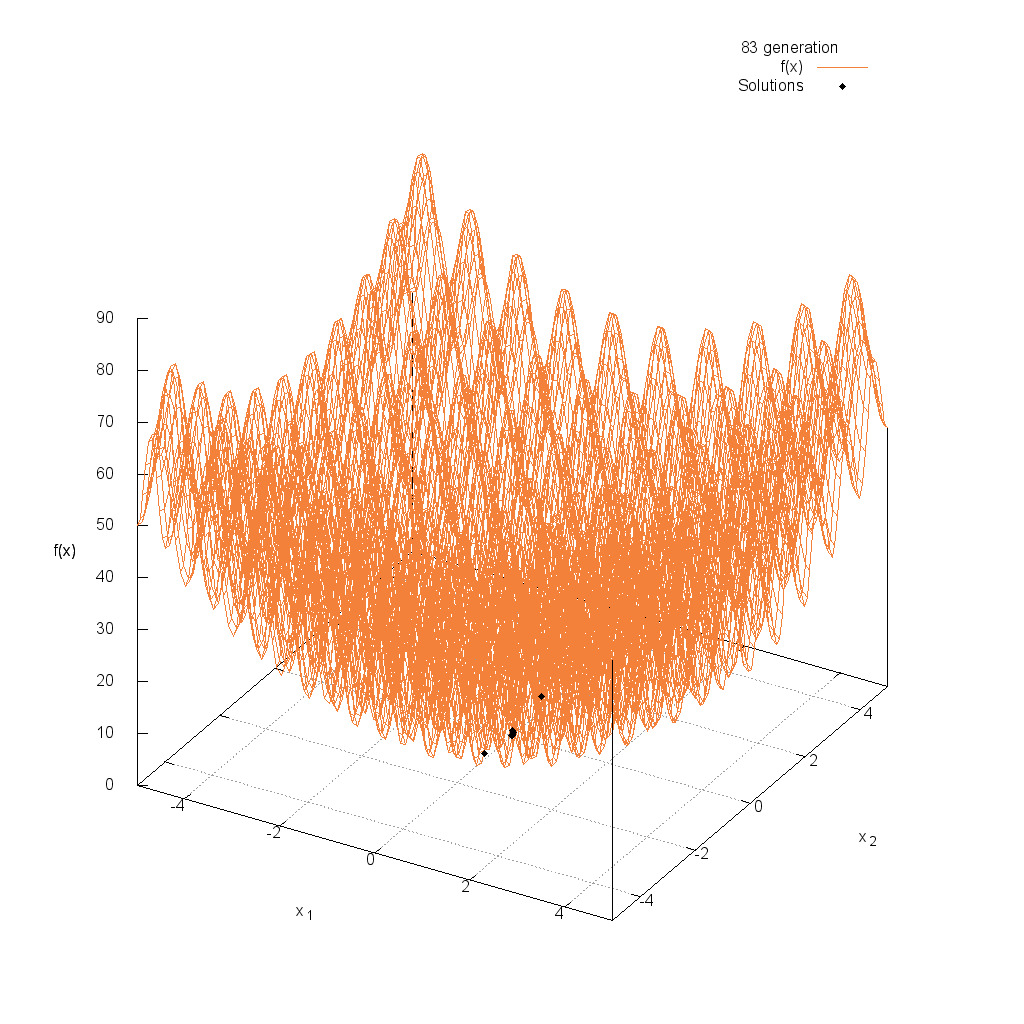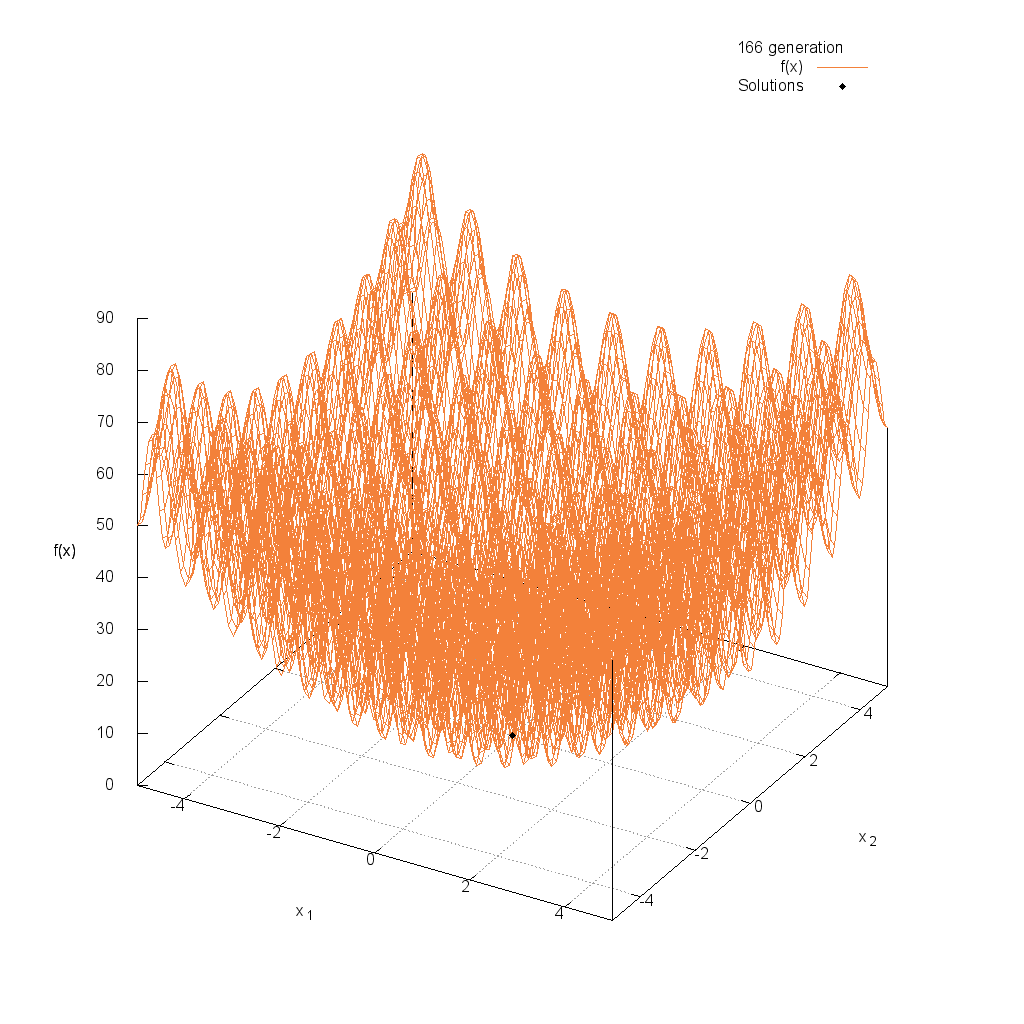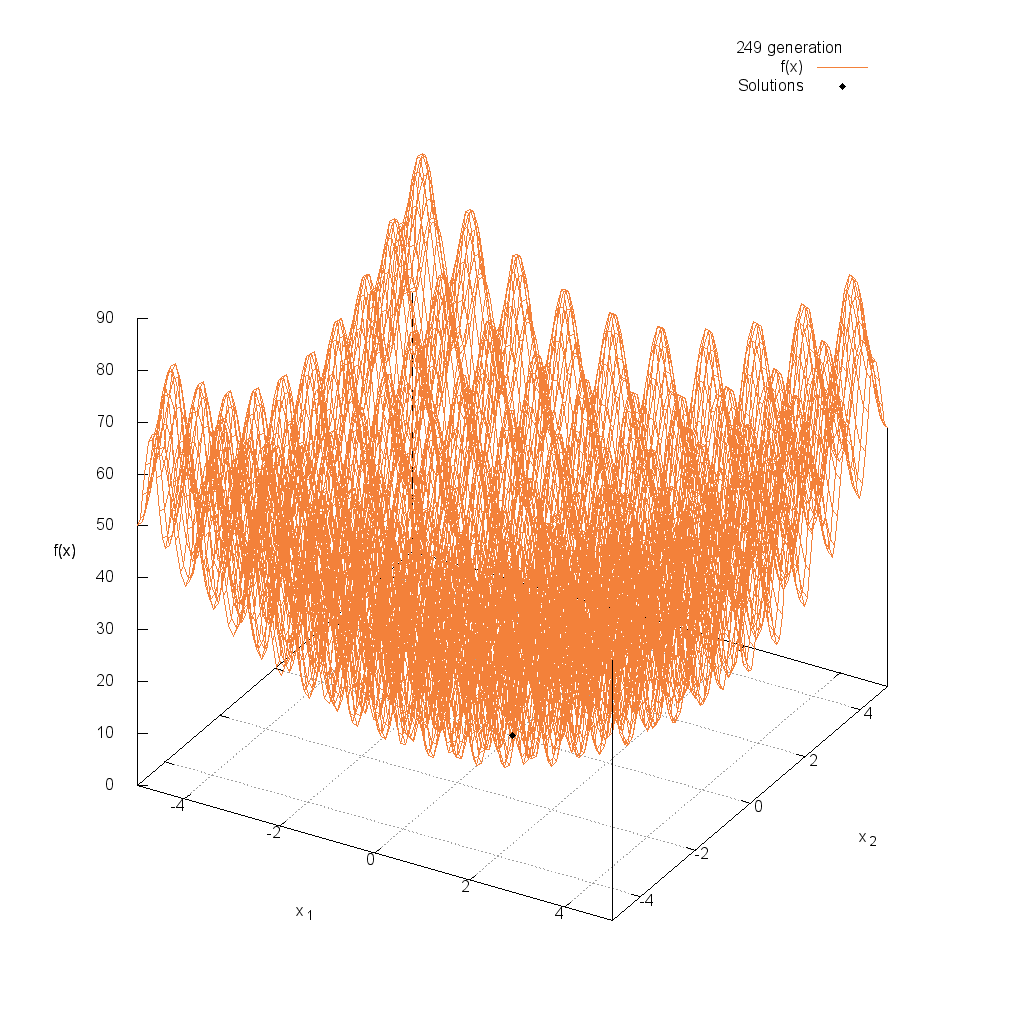
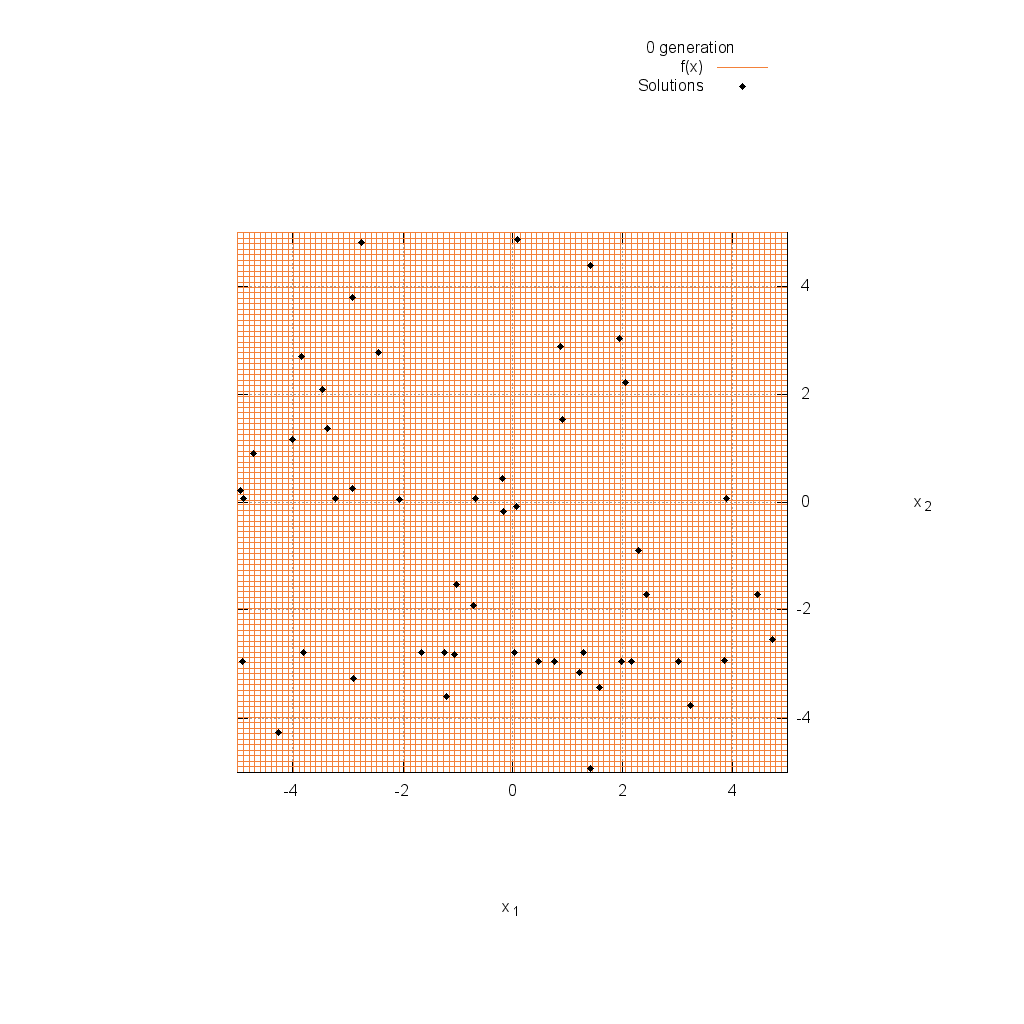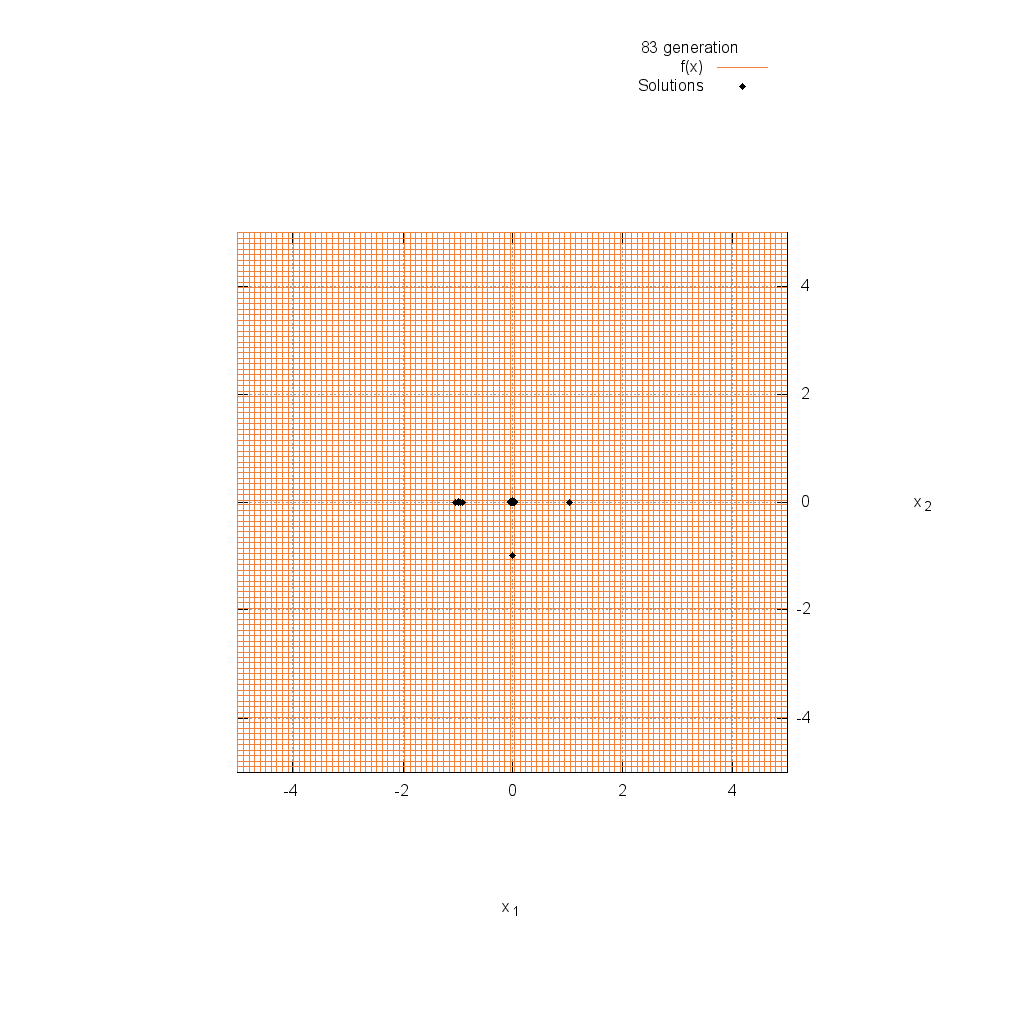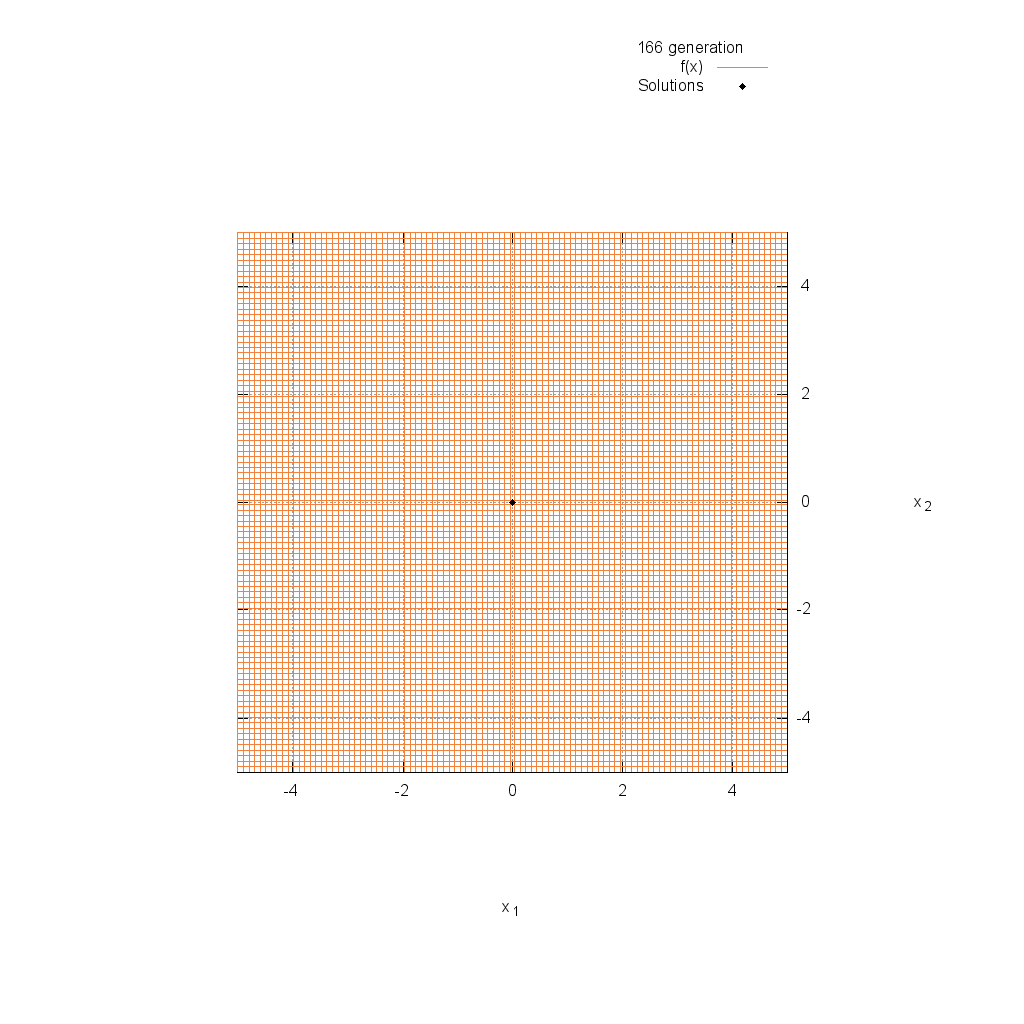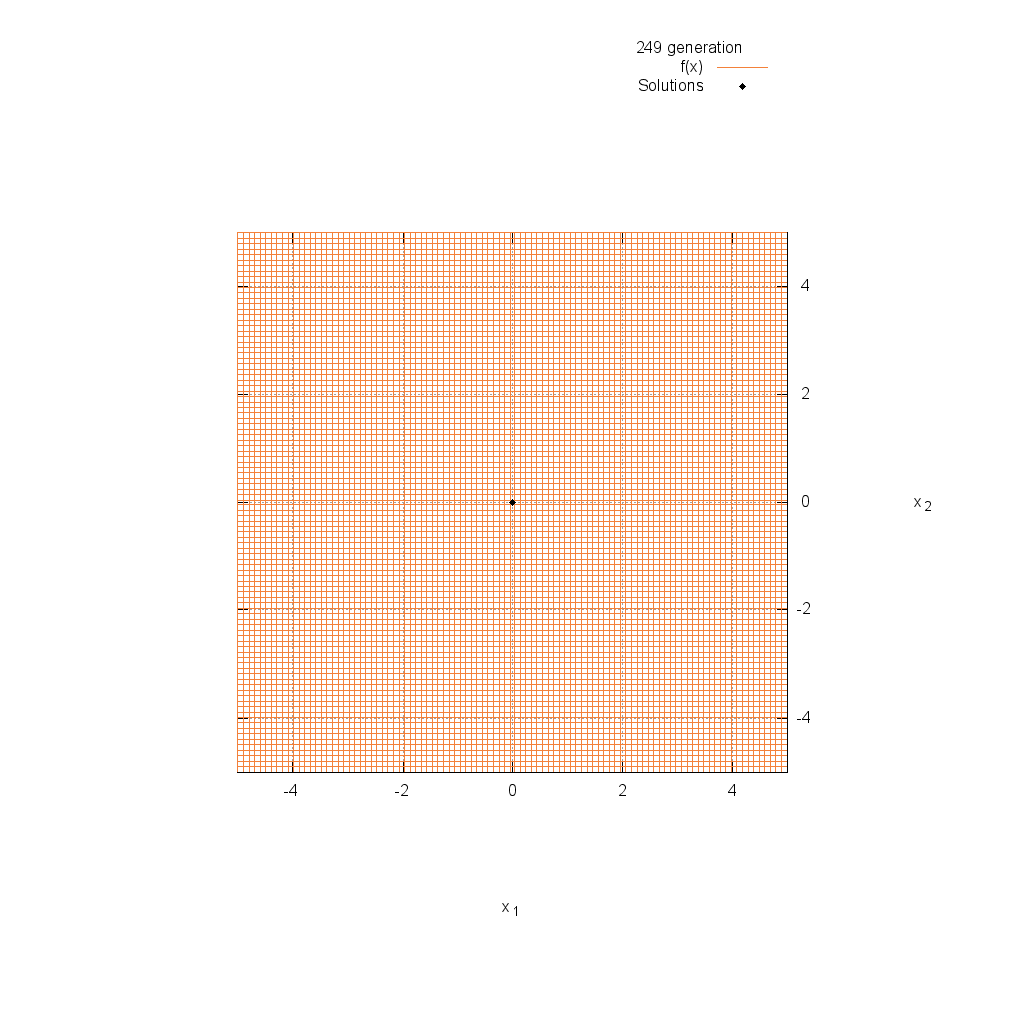
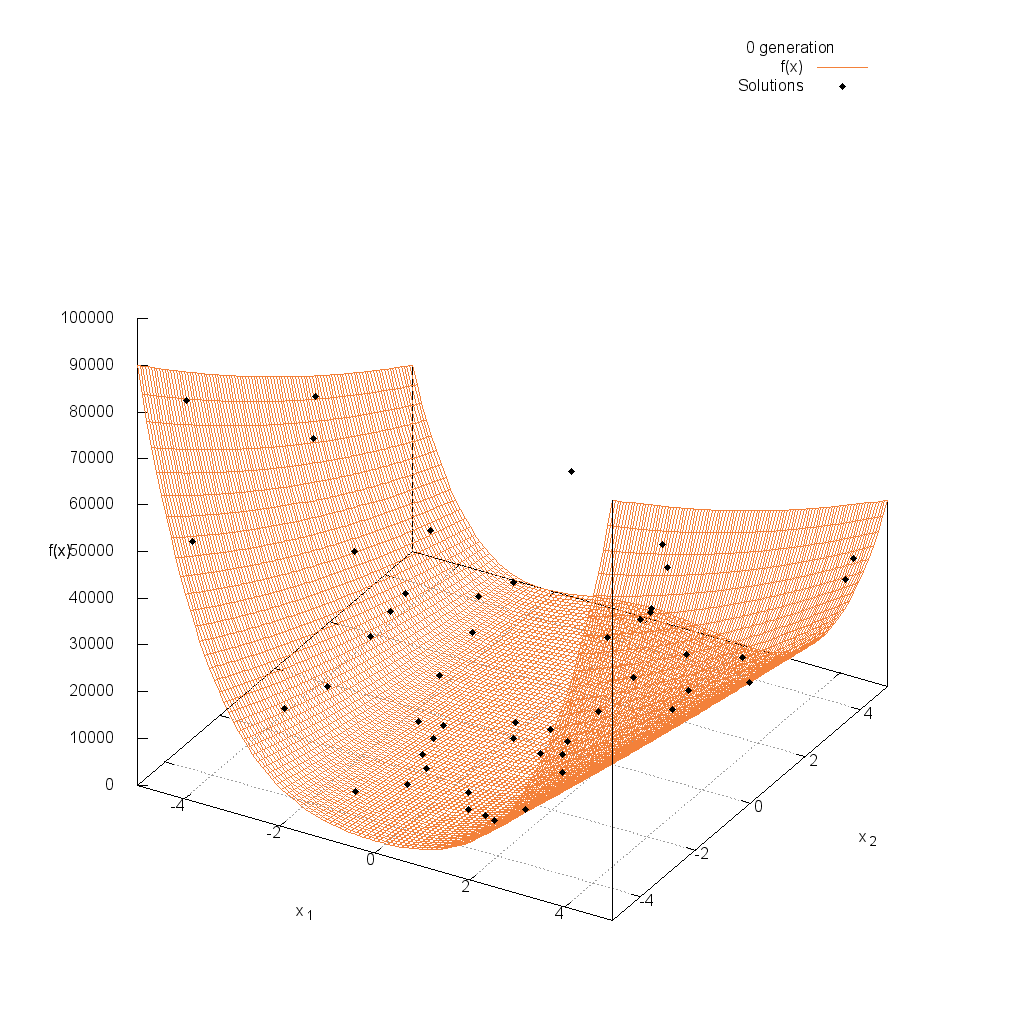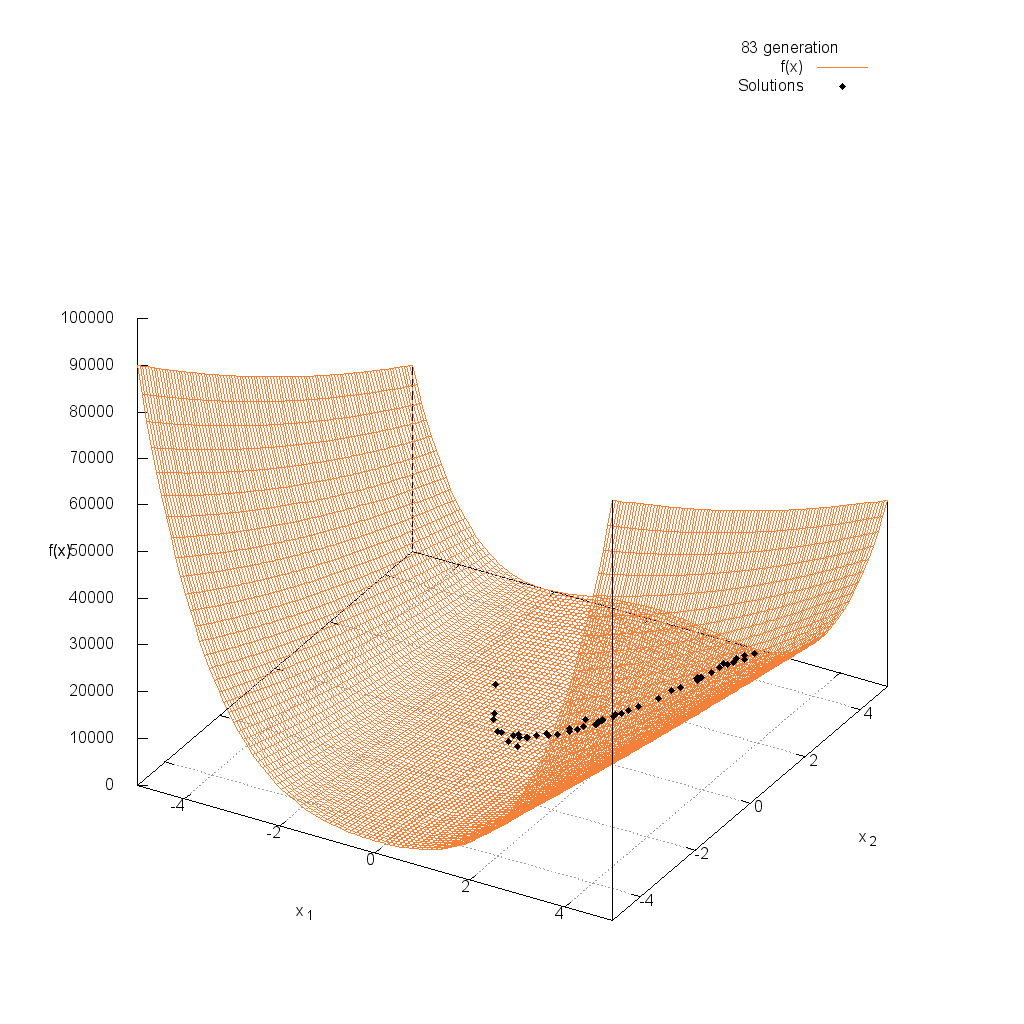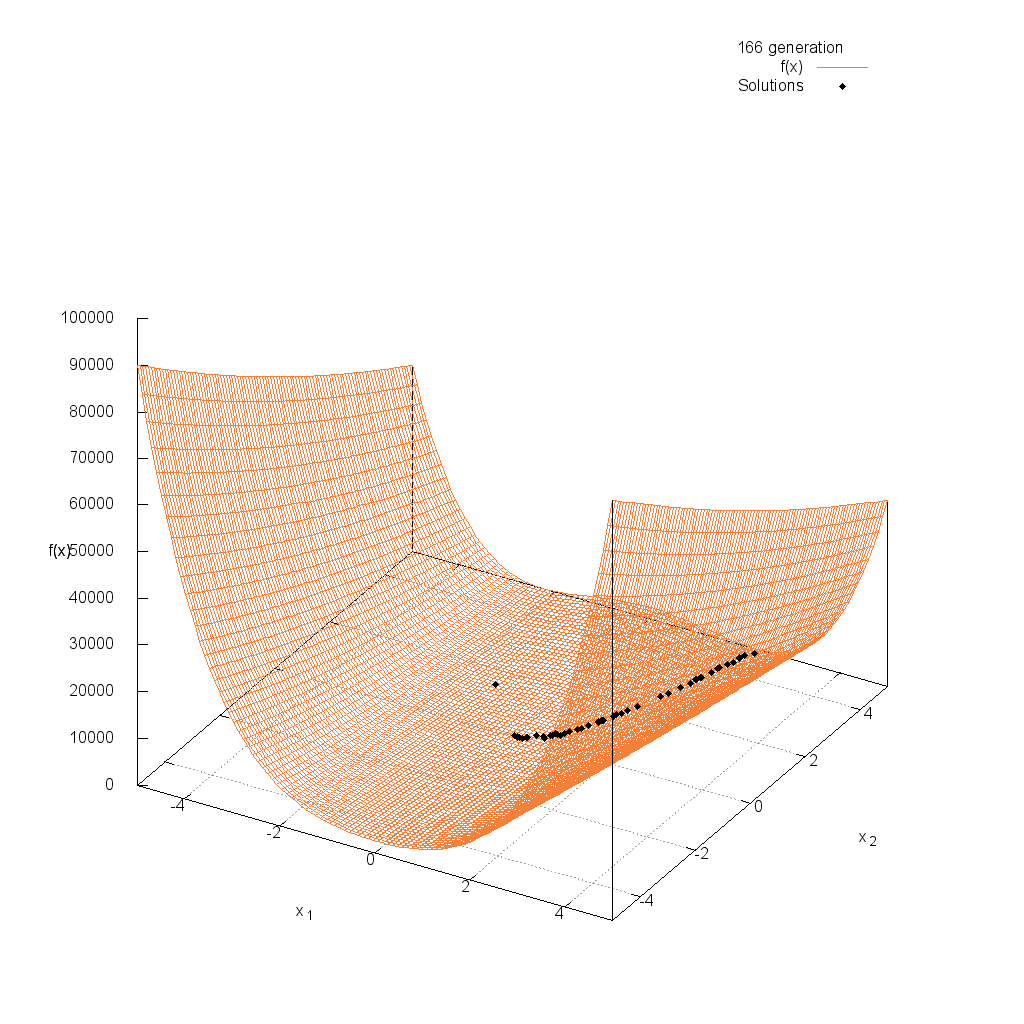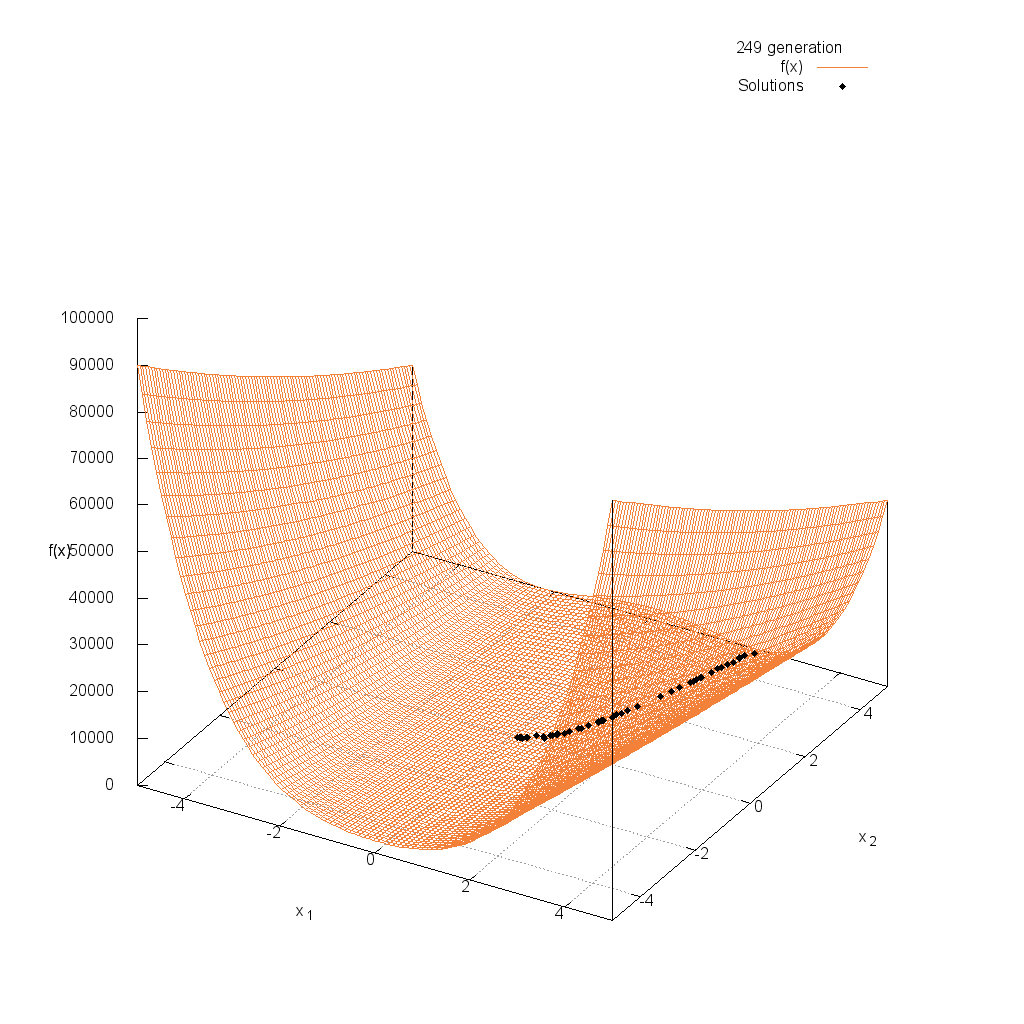
Rosenbrock関数
関数
$$\text{Minimize } f(\boldsymbol{x}) = \sum_{i=1}^{n-1} (100(x_i^2 – x_{i+1})^2 + (1-x_i)^2)$$
$$5.0 \leq x_i \leq 5.0$$